A conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

Net torque applied by the tension in strings can be related as
3BVr2R
BVr2R
BVr23R
BVr22R
The correct Answer is:b
PC and CQ are in parallel. So, equivalent resistance of the
circuit is R/2. In static condition , current through the battery is
I=2V/R.
The current through CP and CQ is i=I/2=V/R
Hence, F1=F2=Bir
Consider the FBD of ring and the blocks
FBD of ring: Consider torque about 'C',
T1r+F1r/2+F2r/2=T2r....(i)
FBD of blocks : T1=mgandT2=mg
So, mgr+Bir2/2+Bir2/2=2mgr
or i=mgBrorVR=mgBrorV=mgRBr
Net torque of tension
=(T2−T1)r=mgr=BVr2R
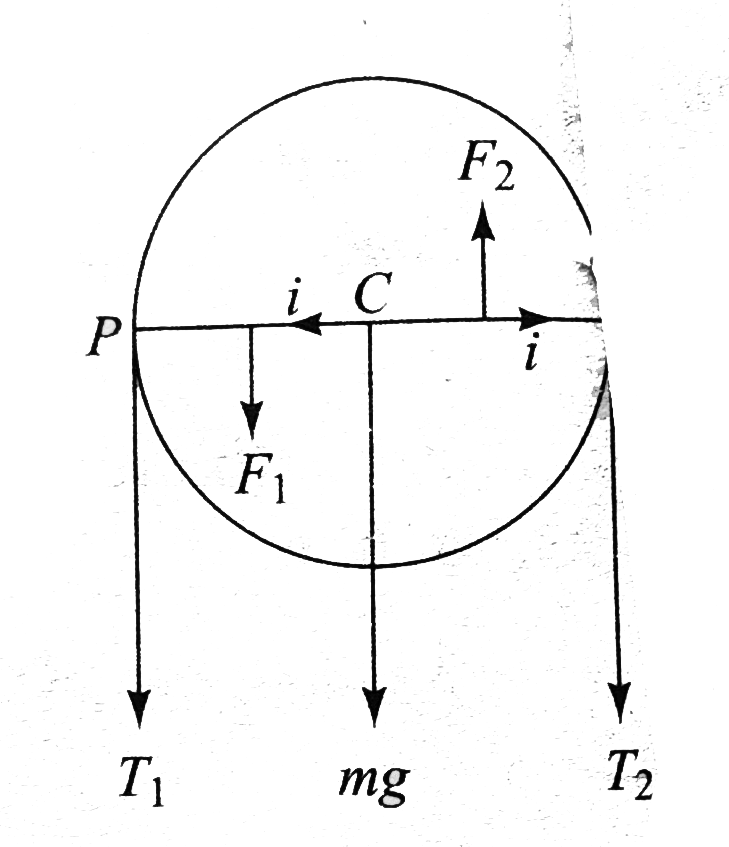
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Integer7videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank6videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning8videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
A conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

The value of V can be related with m, B and r asView SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

The value of V can be related with m, B and r asView SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

In static condition, find the current through rod PC.View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png) View Solution
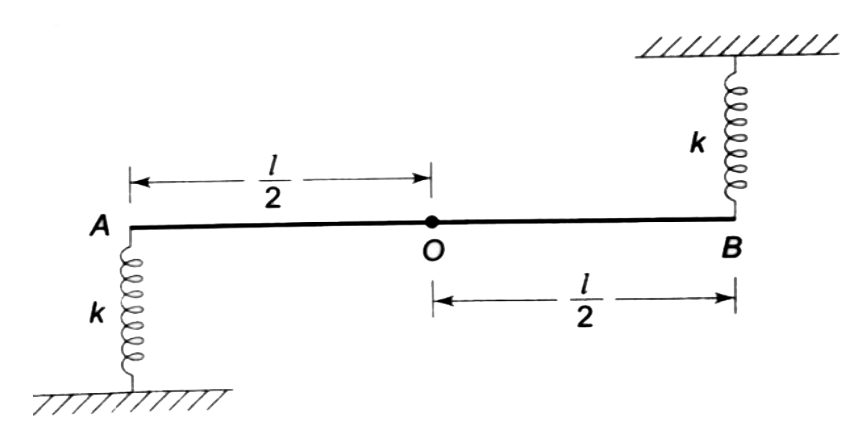
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
 View Solution
View Solution

