A thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5kg is tied and a block of mass 8.0kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0kg to 1.0kg, what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
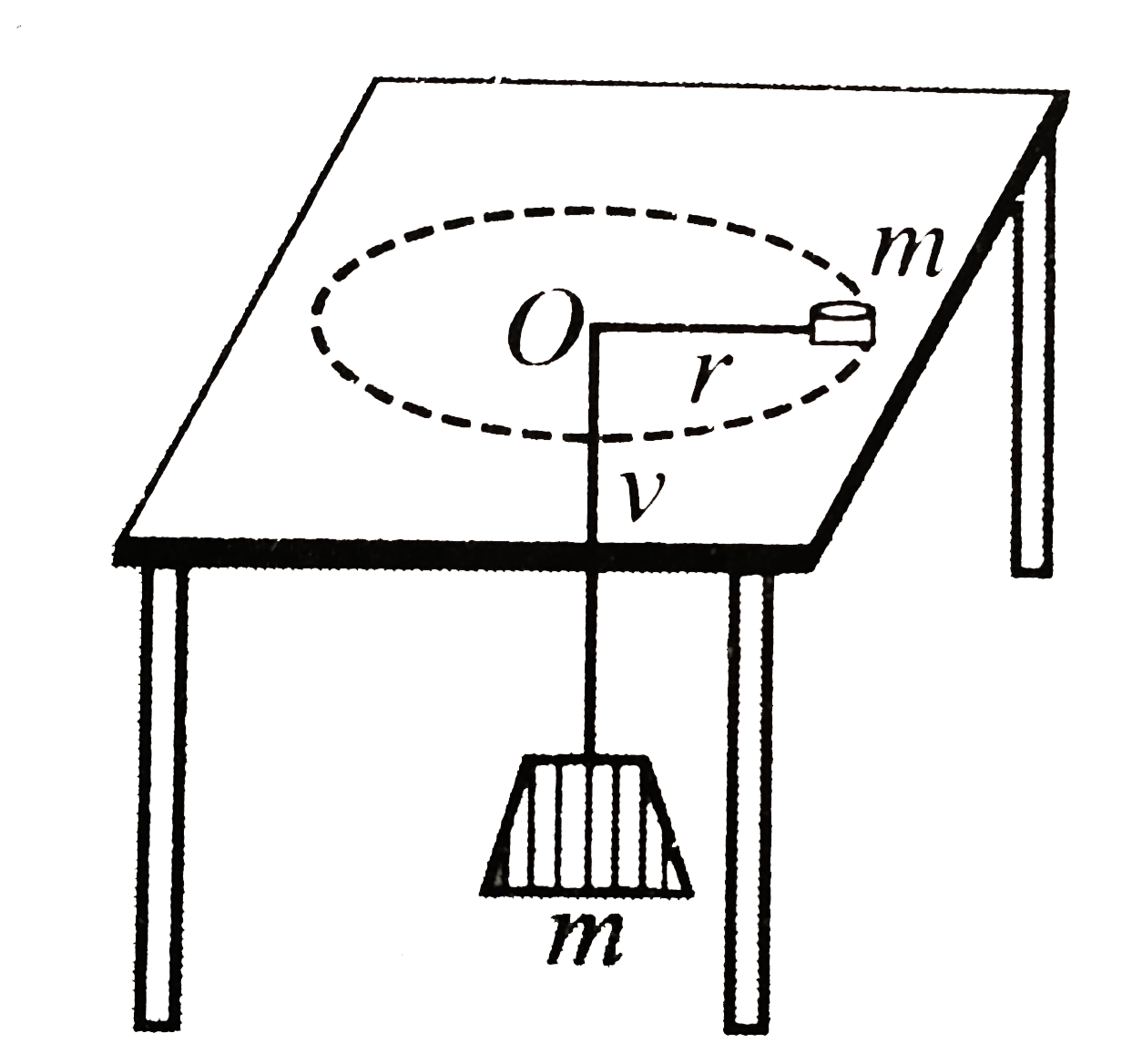
For circular motion of a body tied to a string on a horizontal plane
(mv2r)=T
Here as tension is provided by the hanging mass M.
i.e., T=g, therefore
So,(mv2r)=Mg
According to the given problem,
(mv21/r1)(mv22/r2)=M1gM2g=81 ...........i
Now as force T is central, so angular momentum is also conserved i.e.,
mv1r1=mv2r2..........ii
So substituting the value of v1/v2 from Eq. i Eq. i
[r2r1]×r2r1=81.............iii
i.e., r2r1=2
so that △rr1=r2−r1r1=r2r1−1=2=1
Furthermore as in circular motion v=rω
so, ω2ω1=v2v1×r2r1=[r1r2]2
[as from Eq. ii v2v1=[r1r2]
⇒ω1ω2=[12]2=14
[as from eq. iii r2r1=2]
So, △ωω=ω2−ω1ω1=ω2ω1=1=14−l=−34
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionA rod of length l and mass m is capable of rotating freely about an axis passing through a hole at the end. The period of oscillation of this physical pendulum is
View Solution
Knowledge Check
A uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
Aml2ωBml2ω3Cml2ω12Dml2ω6A block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g=10ms−2)
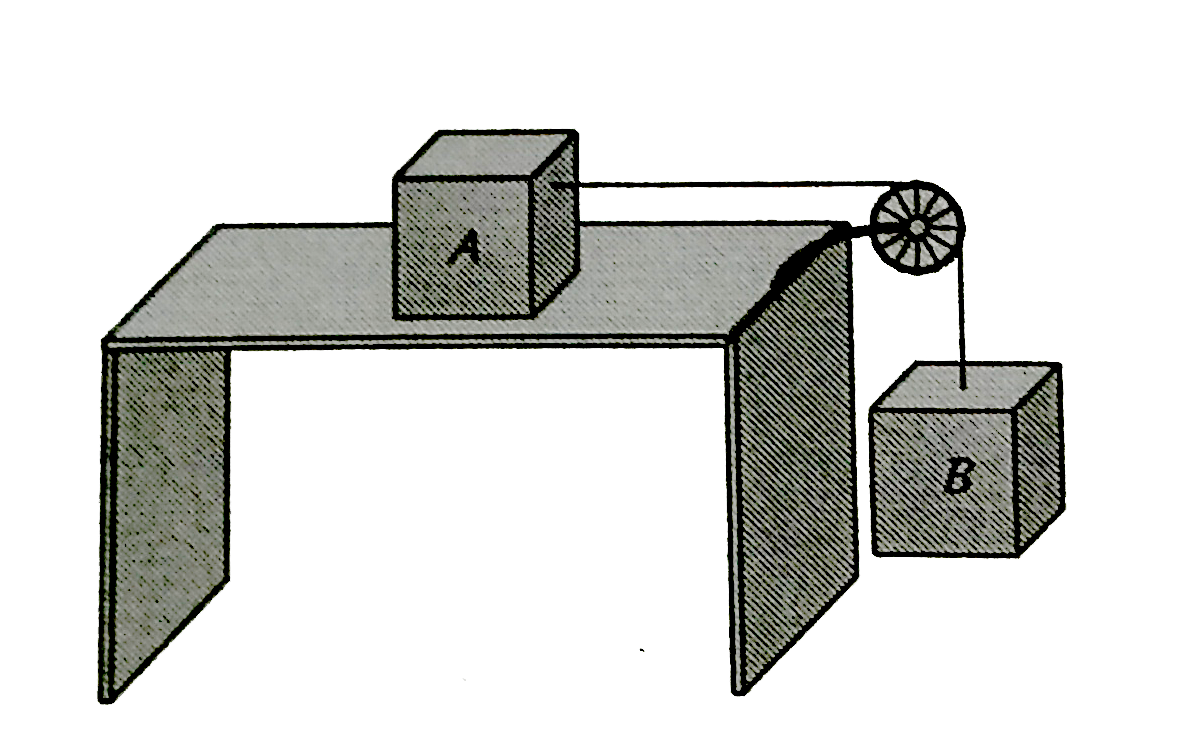 A100ms−2B3ms−2C10ms−2D30ms−2
A100ms−2B3ms−2C10ms−2D30ms−2A uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
Aω06Bω05C4ω05D5ω06
A rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View SolutionA light string passes over a frictionless pulley. To one of its ends a mass of 6 kg is attached. To its other end a mass of 10 kg is attached. The tension in the thread will be
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionMoment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
View SolutionTwo bodies of mass 1 kg and 2 kg are attached to the ends of a 2 metre long weight less rod . This system is rotating about an axis passing through middle point of rod . Calculate M. I of system .
View Solution
