Moment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
ML26
ML212
7ML224
7ML248
The correct Answer is:D
I=ICM+Mx2

ML212+M[L4]2
=ML212+ML216=7ML248
Topper's Solved these Questions
Similar Questions
Find the radius of gyrational and moment of inertia of a rod of mass 100g and length 1m about an axis passing through its centre and perpendicular to its length.
View SolutionFind the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View Solution
Knowledge Check
Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
Aml212Bml23C7ml248Dml29The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
AI0+ML2/4BI0+2ML2CI0+ML2DI0+ML2/2The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0 . Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is
AI0+ML2/2BI0+ML2/4CI0+2ML2DI0+ML2
Calculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
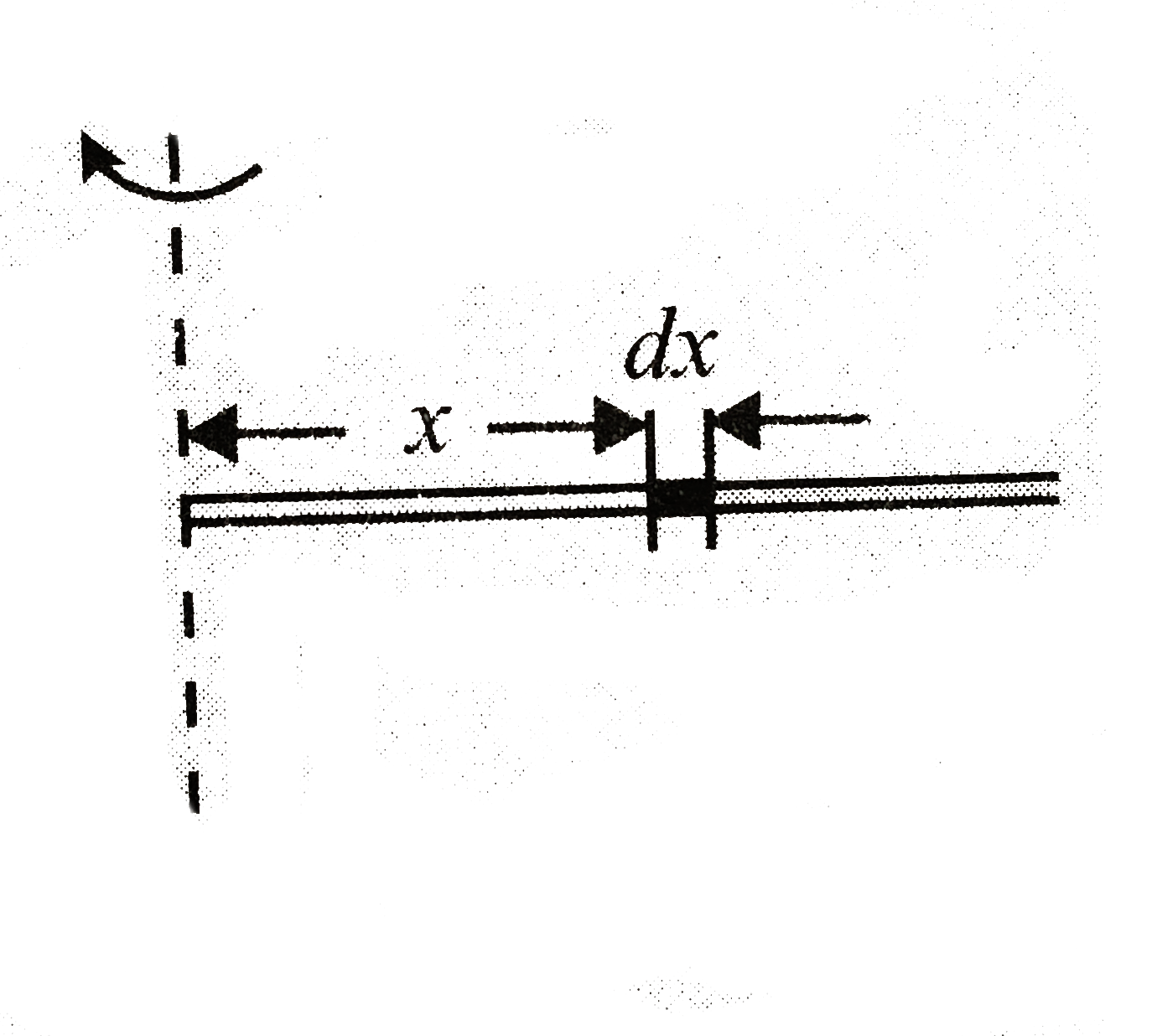
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionMoment of inertia of a thin rod of a mass M and length L about an axis passing through its centre isML212. Its moment of inertia about a parallel axis at a distance of (L)/(4) from this acis is given by
View SolutionMoment of inertia of a rod of mass 'M', length ? about an axis perpendicular to it through one end is,
View Solution