A total reflecting right angled isosceles prism can be used to deviate a ray of light through :
30∘
60∘
75∘
90∘
The correct Answer is:D
To solve the problem of how much a total reflecting right-angled isosceles prism can deviate a ray of light, we can follow these steps:
1. Understanding the Prism:
A right-angled isosceles prism has two equal angles of 45 degrees and one right angle (90 degrees).
2. Incident Ray:
Consider a ray of light striking the first face of the prism. If the ray strikes the surface at a 90-degree angle (perpendicular to the surface), it will pass through without any deviation.
3. Refraction at the First Surface:
Upon entering the prism, the ray will make an angle of 45 degrees with the normal at the second surface (since the internal angle of the prism is 90 degrees).
4. Total Internal Reflection:
The critical angle for glass is approximately 42 degrees. Since the angle of incidence at the second surface is 45 degrees (which is greater than the critical angle), total internal reflection occurs.
5. Refraction at the Second Surface:
After total internal reflection, the ray will reflect off the second surface and again make an angle of 45 degrees with the normal as it exits the prism.
6. Calculating the Total Deviation:
The total deviation of the ray can be calculated as follows:
- The ray is deviated by 45 degrees when it hits the second surface and reflects back.
- It is then deviated again by 45 degrees when it exits the prism.
- Therefore, the total deviation = 45 degrees + 45 degrees = 90 degrees.
7. Conclusion:
The total deviation of the ray of light through a total reflecting right-angled isosceles prism is 90 degrees.
Final Answer:
The total reflecting right-angled isosceles prism can be used to deviate a ray of light through 90 degrees.
---
A right-angled isosceles prism has two equal angles of 45 degrees and one right angle (90 degrees).
Consider a ray of light striking the first face of the prism. If the ray strikes the surface at a 90-degree angle (perpendicular to the surface), it will pass through without any deviation.
Upon entering the prism, the ray will make an angle of 45 degrees with the normal at the second surface (since the internal angle of the prism is 90 degrees).
The critical angle for glass is approximately 42 degrees. Since the angle of incidence at the second surface is 45 degrees (which is greater than the critical angle), total internal reflection occurs.
After total internal reflection, the ray will reflect off the second surface and again make an angle of 45 degrees with the normal as it exits the prism.
The total deviation of the ray can be calculated as follows:
- The ray is deviated by 45 degrees when it hits the second surface and reflects back.
- It is then deviated again by 45 degrees when it exits the prism.
- Therefore, the total deviation = 45 degrees + 45 degrees = 90 degrees.
The total deviation of the ray of light through a total reflecting right-angled isosceles prism is 90 degrees.
The total reflecting right-angled isosceles prism can be used to deviate a ray of light through 90 degrees.
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D)
30 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
- REFRACTION THROUGH A LENS BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
Show with the help of a diagram how a total reflecting prism can be used to turn a ray of light through 90∘. Name one instrument in which such a prism is used.
View SolutionDraw a ray diagram to show a right angled isosceles prism may be used to ''bend the path of light rays by 90∘.
Write the necessary condition in terms of the refractive index of the material of this prism for the ray to bend to 90∘.
View Solution
Knowledge Check
A total reflecting equilateral prism can be used to deviate a ray of light through :
A30∘B60∘C75∘D90∘
Show with the aid of a ray diagram, how a right angled isosceles prism can be used to invert the rays. (a) How sould the rays fall on the prism ?
(b) Which phenomenon is responsible for this action of prism? (c) What is the nature of the image in relation to the object ?
View SolutionA ray of light XY passes through a right angled isosceles prism as shown below.
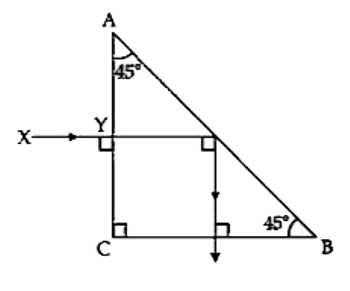
What is the angle through which the incident ray deviates and emerges out of the prism?
View SolutionA ray of light XY passes through a right angled isosceles prism as shown alongside.
What is the angle through which the incident ray deviates and emerges out of the prism ?
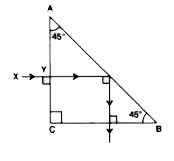
View Solution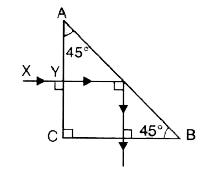
A ray of light XY passes through a right angled isosceles prism as shown alongside Figure.
(a) What is the angle through which the incident ray deviates and emerges out of the prism?
9b) Name the instrument where this action of prism is put into use.
(c) Which prism surface will behave as a mirror ?
View SolutionWrite a relation between the angle of incidence
(i), angle of emergence (e), angle of prism (A) and angle of deviation (d) for a ray of light passing through an equilateral prism.
View SolutionA ray of light XY passes through a right angled isosceles prism as shown below:
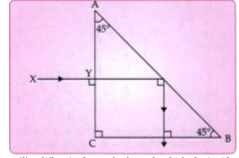
Which prism surface will behave as a mirror ?
View SolutionA ray of light XY passes through a right angled isosceles prism as shown below.
Name the instrument where this action of prism is put into use.
View Solution
