Draw a ray diagram to show a right angled isosceles prism may be used to ''bend the path of light rays by 90∘.
Write the necessary condition in terms of the refractive index of the material of this prism for the ray to bend to 90∘.
Step-by-Step Solution
Step 1: Draw the Right-Angled Isosceles Prism
- Begin by sketching a right-angled isosceles prism. Label the angles: one angle is 90 degrees, and the other two angles are each 45 degrees.
Step 2: Indicate the Incident Ray
- Draw an incident ray approaching the prism at an angle. This ray should strike one of the 45-degree angles of the prism.
Step 3: Draw the Reflected Ray
- After the incident ray strikes the prism, draw the reflected ray that exits the prism at a 90-degree angle to the original path of the incident ray. This means the ray will bend 90 degrees as it passes through the prism.
Step 4: Mark the Normals
- At the point where the incident ray strikes the prism, draw a normal line perpendicular to the surface of the prism. This will help in understanding the angles of incidence and reflection.
Step 5: Apply Snell’s Law
- Use Snell's Law at the interface where the light enters the prism. The condition for total internal reflection must be satisfied for the light to bend by 90 degrees.
Step 6: Establish the Condition for Total Internal Reflection
- For total internal reflection to occur, the angle of incidence must be greater than the critical angle. The critical angle can be determined using the refractive indices of the prism and air.
Step 7: Write the Mathematical Condition
- The necessary condition in terms of the refractive index (μ) of the prism is given by:
μsin(45∘)>sin(90∘)
Since sin(45∘)=1√2 and sin(90∘)=1, we can rewrite the inequality as:
μ⋅1√2>1
Therefore, rearranging gives:
μ>√2
Final Answer
- The ray diagram shows how a right-angled isosceles prism can bend the path of light rays by 90 degrees. The necessary condition for this to occur is that the refractive index of the material of the prism must be greater than √2.
- Begin by sketching a right-angled isosceles prism. Label the angles: one angle is 90 degrees, and the other two angles are each 45 degrees.
- Draw an incident ray approaching the prism at an angle. This ray should strike one of the 45-degree angles of the prism.
- After the incident ray strikes the prism, draw the reflected ray that exits the prism at a 90-degree angle to the original path of the incident ray. This means the ray will bend 90 degrees as it passes through the prism.
- At the point where the incident ray strikes the prism, draw a normal line perpendicular to the surface of the prism. This will help in understanding the angles of incidence and reflection.
- Use Snell's Law at the interface where the light enters the prism. The condition for total internal reflection must be satisfied for the light to bend by 90 degrees.
- For total internal reflection to occur, the angle of incidence must be greater than the critical angle. The critical angle can be determined using the refractive indices of the prism and air.
- The necessary condition in terms of the refractive index (μ) of the prism is given by:
μsin(45∘)>sin(90∘)
Since sin(45∘)=1√2 and sin(90∘)=1, we can rewrite the inequality as:
μ⋅1√2>1
Therefore, rearranging gives:
μ>√2
- The ray diagram shows how a right-angled isosceles prism can bend the path of light rays by 90 degrees. The necessary condition for this to occur is that the refractive index of the material of the prism must be greater than √2.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-C8videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-E4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
When a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View Solution
Knowledge Check
- Question 1 - Select One
A total reflecting right angled isosceles prism can be used to deviate a ray of light through :
A30∘B60∘C75∘D90∘
A ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
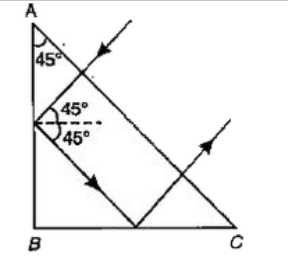 View Solution
View SolutionShow with the aid of a ray diagram, how a right angled isosceles prism can be used to invert the rays. (a) How sould the rays fall on the prism ?
(b) Which phenomenon is responsible for this action of prism? (c) What is the nature of the image in relation to the object ?View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionOne of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
View SolutionIn the diagram the ray passing through prism is parallel to the base. Refractive index of material of prism is
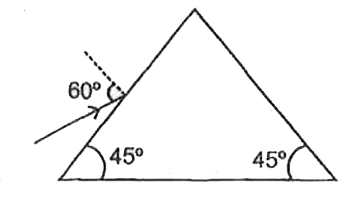 View Solution
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View SolutionA light ray going through a prism with the angle of prism 60∘, is founded to deviate at least by 30∘. what Is the range of the refractive index of the prism?
View Solution

