A track is mounted on a large wheel that is free to turn with neigligible friction about a vertical axis (Fig). A toy train of mass $M$ is placed on the track and, with the system initially at rest, the train's electrical power is turned on. The train reaches speed $v$ with respect to the track. What is the wheel's angular speed if its mass is $m$ and its radius is $r$ ? (Treat it as a hoop, and neglect the mass of the spokes and hub).
.

A

$\frac{v}{(M / m + 1) R}$

B

$\frac{v}{(m / M + 2) R}$

C

$\frac{v}{(M / m + 2) R}$

D

$\frac{v}{(m / M + 2) R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

(b) No external torque acts on the system consisting of the train and wheel, so the total angular momentum of the system (which is initially zero) remains zero.
Let $I = m R^{2}$ be the rotational inertia of the wheel (which we treat as a hoop). Its angular momentum is
${\to L}_{w h e e l} = (I ω) ˆ k = - m R^{2} | ω | ˆ k$
Where $ˆ k$ is up in figure and that last step (with the minus sign) is done in recognition that the wheel's clockwise rotation implies a negative vlaue for $ω$ . The linear speed of point on the track is $- | ω | R$ and the speed of the train (going counterclockwise in figure with the speed $v'$ relative to an outside observer) is therefore $v' = v - | ω | R$ where $v$ is its speed relative to the tracks. Consequently, the angular momentum of the train is ${\to L}_{t r a \in} = M (v - | ω | R) R ˆ k$ . Conservation of angular momentum yields.
$0 = {\to L}_{wheel} + {\to L}_{train} = - m R^{2} | ω | ˆ k + M (v - | ω | R) R ˆ k$
which we can use to solve for $| ω |$
Solving for the angular speed, the result is
$| ω | = \frac{m v R}{(M + m) R^{2}} = \frac{v}{(m / M + 1) R}$ .]

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A train of mass M is moving on a circular track of radius R with constant speed $v$ . The length of the train is half of the perimeter of the track. The linear momentum of the train will be
Azero
B $\frac{2 M v}{π}$
C $M V R$
DMV
Question 2 - Select One
High-speed magnetic levitation trains run without touching the track, on the power of
Aelectromagnets
Bbar magnets
Cnatural magnets
Dnone of these
Question 3 - Select One or More
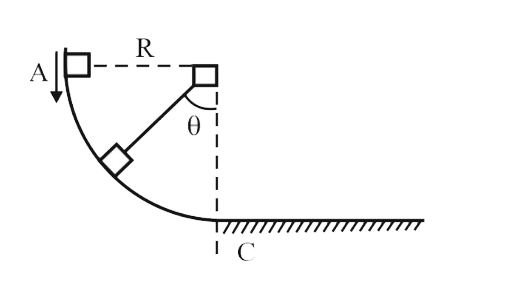
A block of mass m is placed on a circular track and then it is given a velocity $υ$ vertically downwards at position A on track. If block moves on track with constant speed, then

ACoefficient of friction between block and circular track as function of angle $θ$ is $μ = \frac{sin θ}{cot θ + \frac{v^{2}}{R g}}$
BCoefficient of friction between block and circular track as function of angle $θ$ is $μ = \frac{sin θ}{cos θ + \frac{v^{2}}{R g}}$
CInstantaneous power due to friction is $- m g v sin θ$
DWork done from A to C by friction on block will be $- m g R$

A2Z-ROTATIONAL DYNAMICS-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile