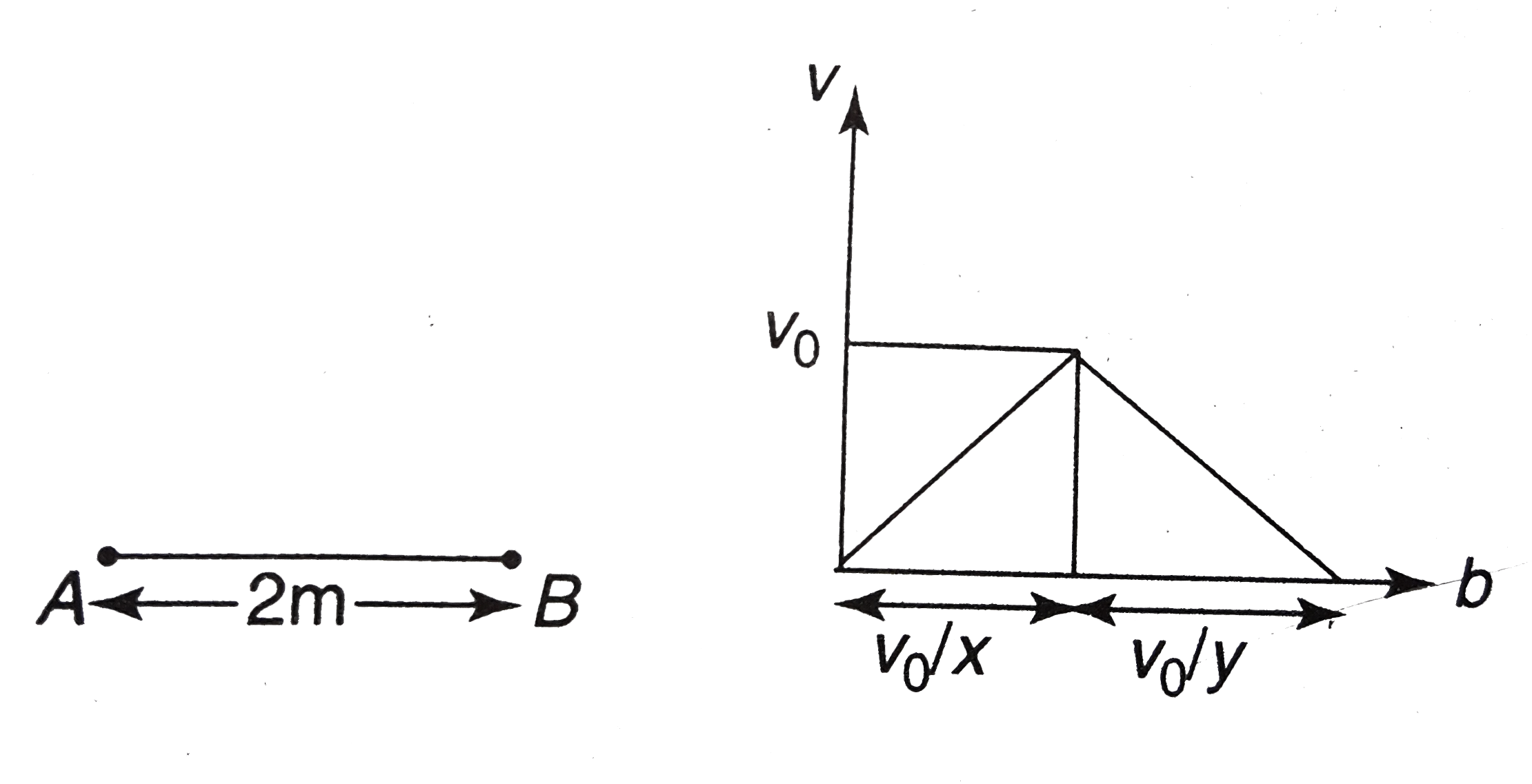
A train stopping at two stations 2 km apart on a straight line takes 4

Topper's Solved these Questions

BOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - AIIMS Questions
20videos
GENERAL KINEMATICS AND MOTION IN ONE DIMENSION
BOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test
29videos
FLUID MECHANICS
BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29videos
GRAVITATION

Knowledge Check

Question 1 - Select One
For $1 / m$ of the distance between two stations a train is uniformly accelerated and for $1 / n$ of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. Then the ratio of its greatest velocity to its average velocity is
A $1 + 1 / m : 1 / n$
B $1 + 1 / m + 1 / n : 1$
C $1 + 1 / n : 1 / m$
DNone of these
Question 2 - Select One
For $\frac{1}{m}$ of the distance between two stations a train is uniformly accelerated and $\frac{1}{n}$ of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. The ratio of the greatest velocity to the average velocity will be:
A $(1 + \frac{1}{m} - \frac{1}{n})$
B $(1 + \frac{1}{m} + \frac{1}{n})$
C $(\frac{1}{m} + \frac{1}{n} - 1)$
D $(\frac{1}{m} + \frac{1}{n})$
Question 3 - Select One
Starting at time t = 0 from the origin with speed $1 m s^{- 1}$ , a particle follows a tow - dimensional trajectory in the x - y plane so that its coordinates are related by the equation $y = \frac{x^{2}}{2}$ . The x and y components of its acceleration are denoted by $a_{x}$ and $a_{y}$ respectively . Then, the incorrect statement is:
A $a_{x} = 1 m s^{- 2}$ implies that when the particle is at the origin $a_{y} = 1 m s^{- 2}$
B $a_{x} = 0$ implies $a_{y} = 1 m s^{- 2}$ at all times
Cat $t = 0$ the paritcles velcoity points in the x - direction
D $a_{x} = 0$ implies that at 1 = 1s the angle between the particle 's velocity and the x aixs is $45^{\circ}$

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

For $1 / m$ of the distance between two stations a train is uniformly accelerated and for $1 / n$ of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. Then the ratio of its greatest velocity to its average velocity is

For $\frac{1}{m}$ of the distance between two stations a train is uniformly accelerated and $\frac{1}{n}$ of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. The ratio of the greatest velocity to the average velocity will be:

A2Z-GENERAL KINEMATICS AND MOTION IN ONE DIMENSION-Chapter Test

A train stopping at two stations 2km apart on a straight line takes 4 minutes for the journey. Assuming that its motion its uniformly accelerated and then unoformly retarded. If 1x+1y=n, where 'x' and 'y' are the magnitudesof the acceleration and retardation respectively. find the value of n.

The correct Answer is:C

Total time taken =4min (i) v0x+v0y=4min (ii) Total distance travelled =2km ⇒ Area under v−t graph =2km 12×v0x×v0+12×v0y×v0=2km From (i) and (ii), 1x+1y=4.

Topper's Solved these Questions

Similar Questions

Knowledge Check

For 1/m of the distance between two stations a train is uniformly accelerated and for 1/n of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. Then the ratio of its greatest velocity to its average velocity is

For 1m of the distance between two stations a train is uniformly accelerated and 1n of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. The ratio of the greatest velocity to the average velocity will be:

A2Z-GENERAL KINEMATICS AND MOTION IN ONE DIMENSION-Chapter Test

For $1 / m$ of the distance between two stations a train is uniformly accelerated and for $1 / n$ of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. Then the ratio of its greatest velocity to its average velocity is

For $\frac{1}{m}$ of the distance between two stations a train is uniformly accelerated and $\frac{1}{n}$ of the distance it is uniformly retarded. It starts from rest at one station and comes to rest at the other. The ratio of the greatest velocity to the average velocity will be: