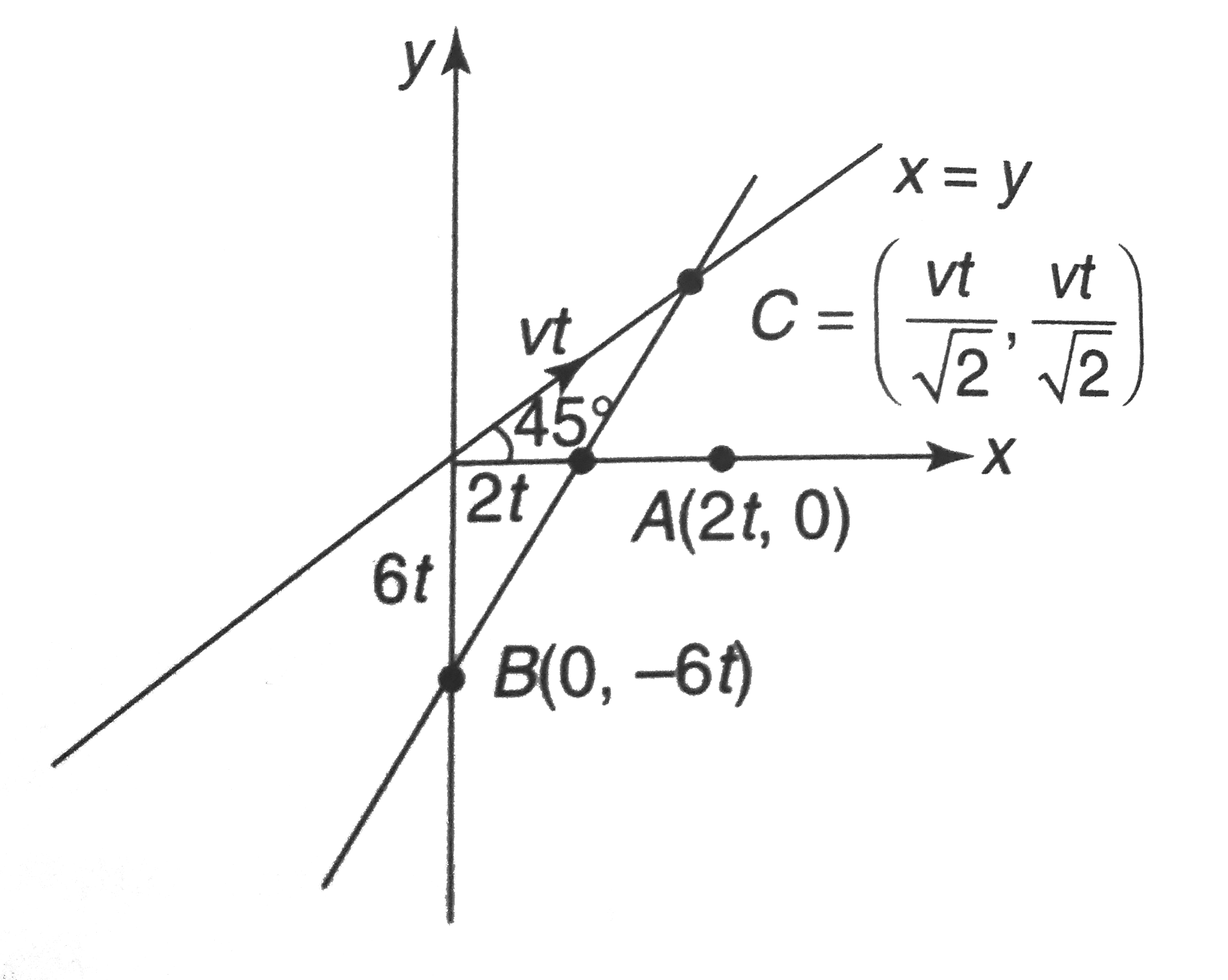
Three particles starts from origin at the same time with a velocity 2ms−1 along positive x-axis, the second with a velocity 6ms−1 along negative y-axis, Find the velocity of the third particle along x=y line so that the three particles may always lie in a straight line.
−3√3
3√2
−3√2
2√2
The correct Answer is:B
Slope AB= slope AC
2t−00+6t=2t−vt√20−vt√2
Solve to get v=3√2m/s.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - AIIMS Questions
20 Videos
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
Similar Questions
Three particles start from the origin at the same time, one with velocity u1 along the x-axis, the second with velocity u2 along the y-axis . Find the velocity of the third particles, along the x=y line so that the three particles may always lie on the same straight line.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
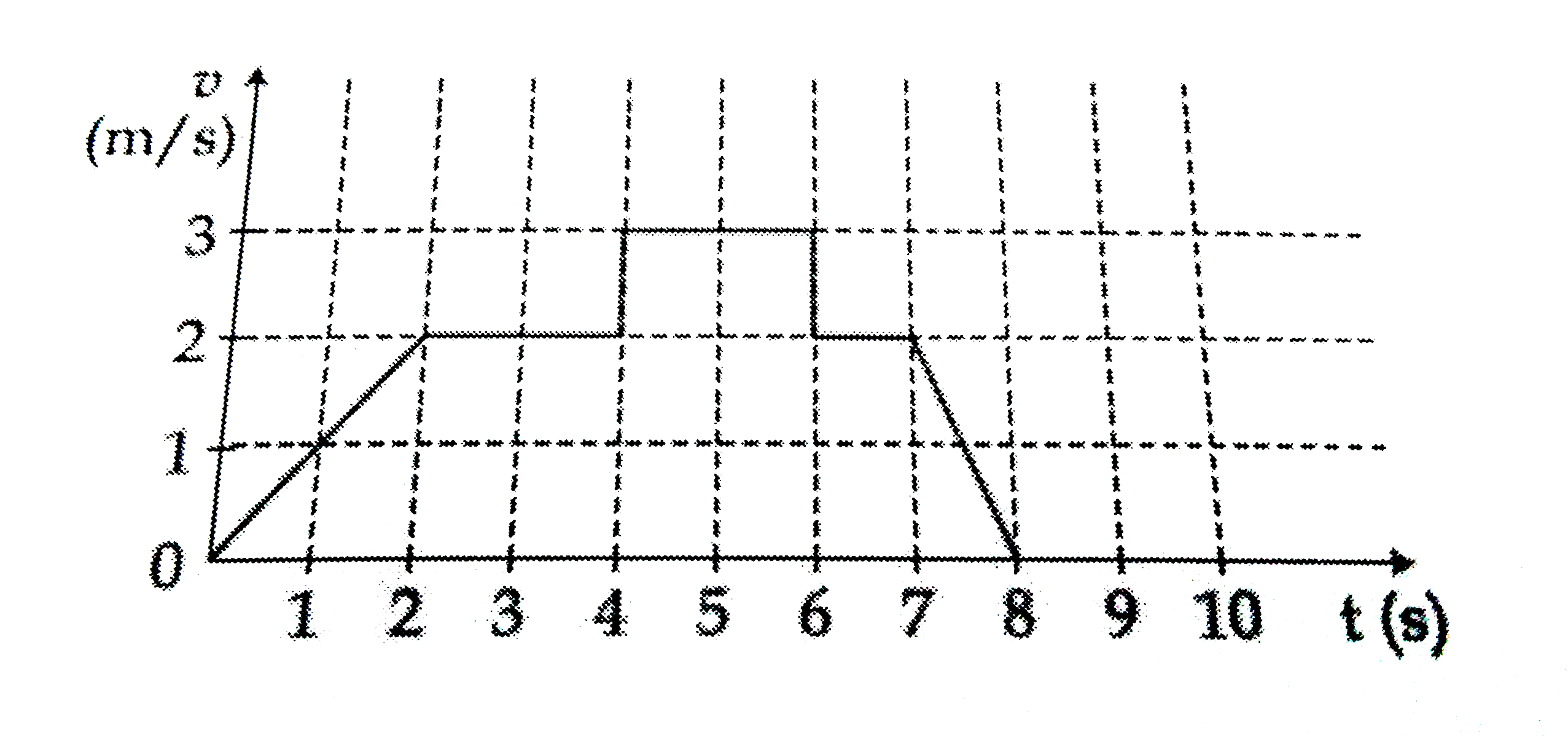
View Solution
Knowledge Check
Three particles start from the origin at the same time, one with a velocity v1 along the x-axis, second along the negative y-axis with a velocity v2 and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
Av1+v22B√v1+v2Cv1v2v1+v2Dv=√2v1v2v1−v2Three particles start from origin at the same time: one with velocity v1 along positive x-axis, the second along the positive y-axis with a velocity v2 and the third along the line y = x with such a speed that all the three always stay in a straight line, then velocity of the third particles is:
A√v1v2Bv1+v22Cv1v2√v21+v22Dv1v2√2v1+v2Three particles A,B and C start from the origin at the same time,A with a velocity a along x-axis, B with a velocity b along y-axis and C with velocity c in XY plane along the line x=y.The magnitude of c so that the three always remain collinear is:
Aa+b2B√abCaba+bD√2aba+b
A particle P is moving along a straight line with a velocity of 3ms−1 and another particle Q has a velocity of 4ms−1 at an angle of 30∘ to the path of P. Find the speed of Q relative to P.
View SolutionA body starts from the origin with an acceleration of 6ms−1 along the x - axis and 8ms−1 along the y - axis. Find its distance from the origin after 4s.
View SolutionA particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionA particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View Solution
