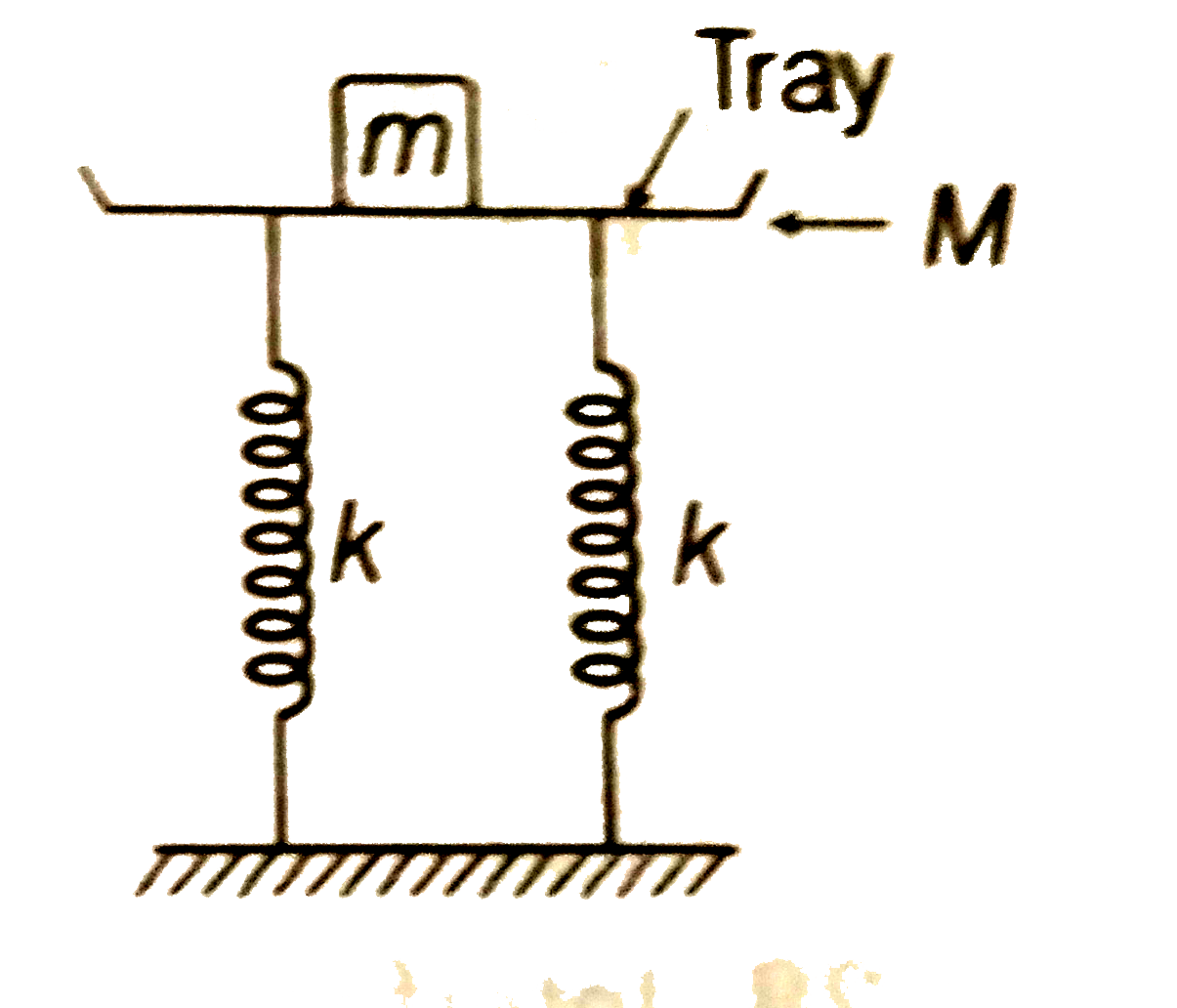
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a blockof mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m is
10 kg
20 kg
30 kg
40 kg
The correct Answer is:C
There are two identical springs which are connected in parallel, ltBrgt ∴ The effective spring consistant of the combination is
k'=k+k=2k
∴ Time period
T=2π√Mk'=2π√M2k . . . (i)
when block of mass m is placed in the tray, the period of oscillation becomes
T'=2π√M+mk'=2π√M+m2k . . . (ii)
Divide (ii) by (i), we get
T'T=√M+mM⇒31.5=√10+m10
On squaring both sides, we get
4=10+m10 or 40=10+m
or m=30 kg.
Topper's Solved these Questions
Similar Questions
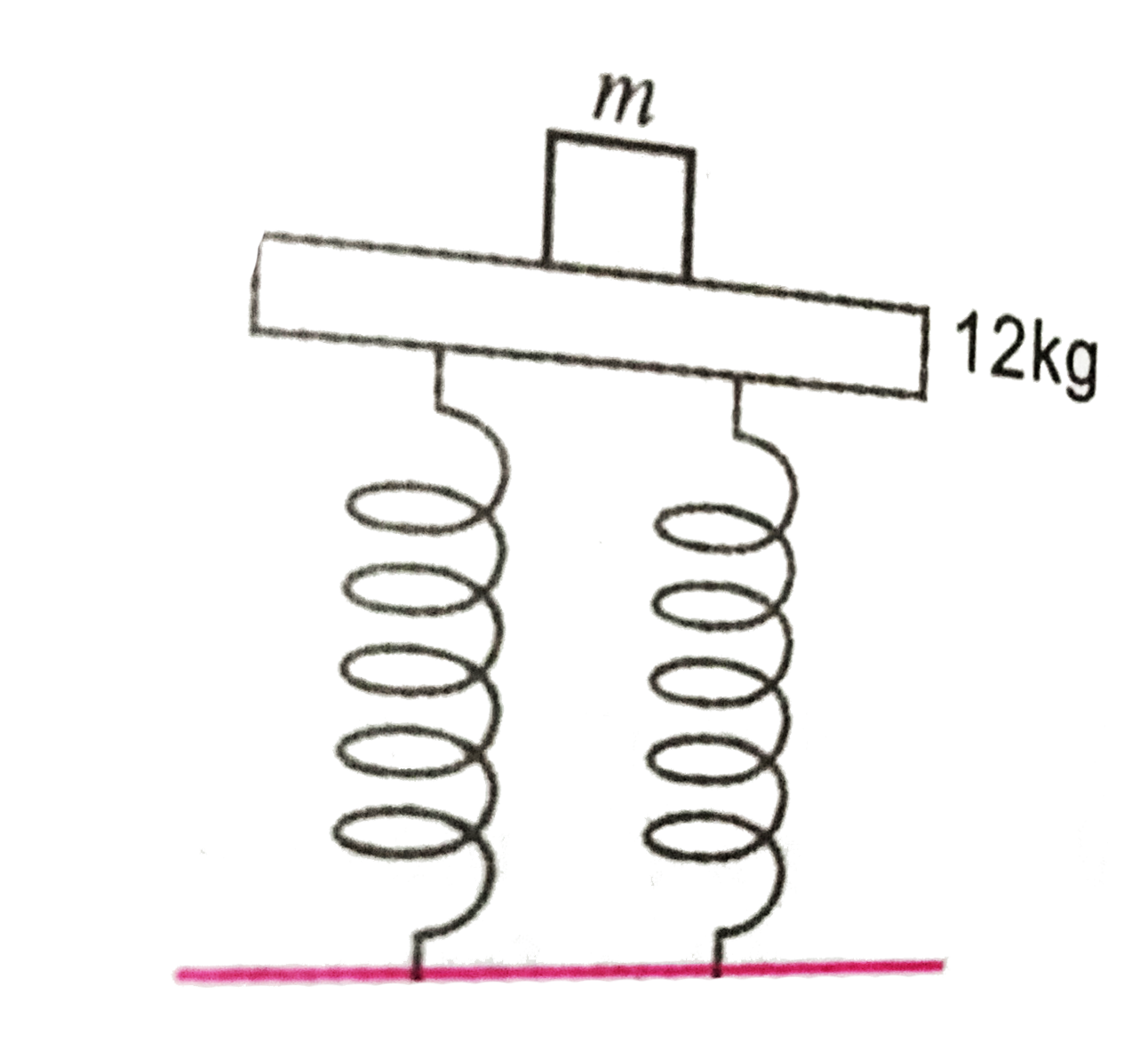
A tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View Solution
Knowledge Check

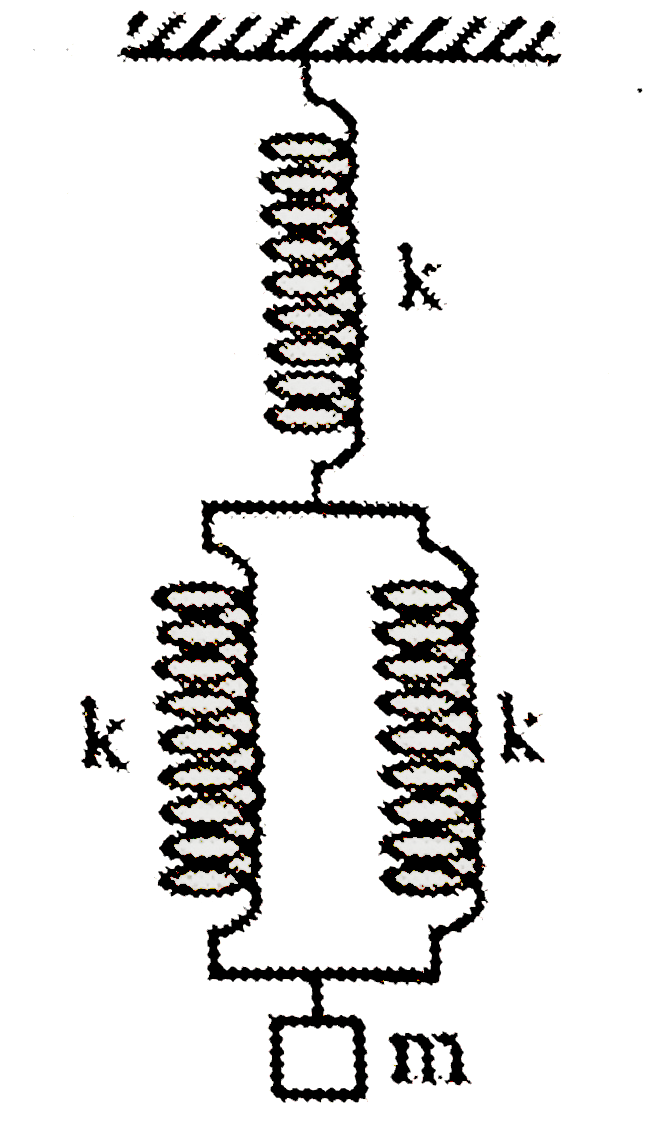
A plank of mass 12 kg is supported by two identical springs as shown is Fig. The plank always remains horizontal. When the plank is pressed down and released it performs simple harmonic motion with time period 3 s. When a block of m is attached to the plank the time priod changes to 6 s. The mass of the block isA48 kgB36 kgC24 kgD12 kgA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA body of mass m = 2kg hangs from three springs, each of spring constant 1875 N/m, as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period
 Aπ5 secBπ25 secC2π5secD2π25 sec
Aπ5 secBπ25 secC2π5secD2π25 sec
A solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.

View SolutionA tray of mass M = 10 kg executes SHM of period 1.5s. It is supported on two identical springs of spring constant k as shown in figure. If a block of mass m is also placed on the tray, the period of oscillation increases to 3s. The value of m is:
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View Solution
