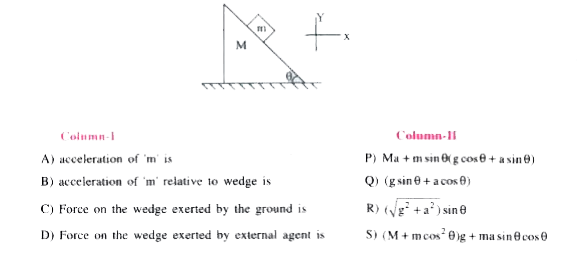
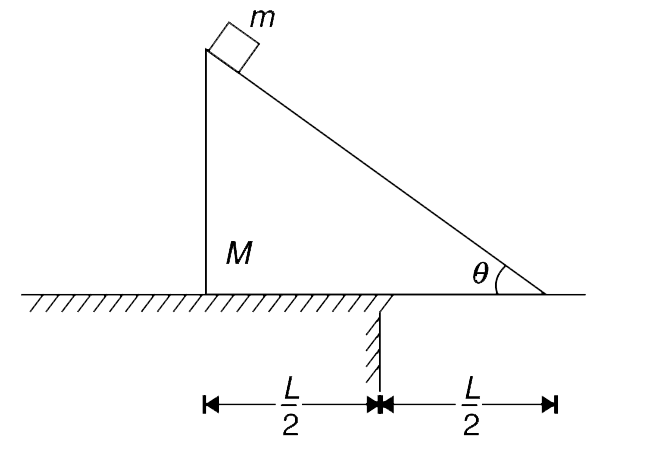
A triangular wedge of mass M lies on a smooth horizontal table with half of its base projecting out of the edge of the table. A block of mass m is kept at the top of the smooth incline surface of the wedge and the system is let go. Find the maximum value of Mm for which the block will land on the table. Take θ=60∘.
The correct Answer is:3
Topper's Solved these Questions
Similar Questions
Knowledge Check
A block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
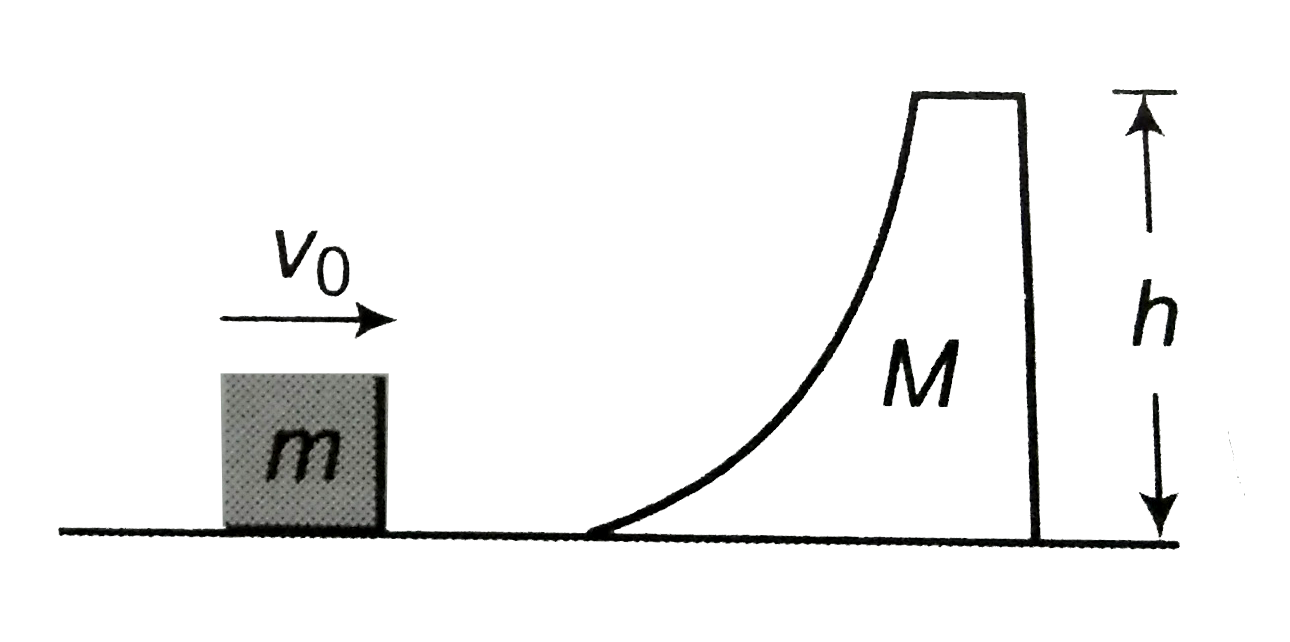 A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)A small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
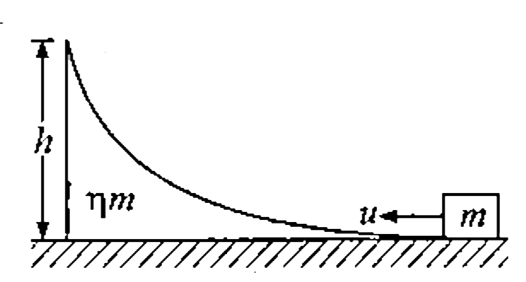 A√2gh(1+1h)B√(1+12gh)nC√n2ghD√1+h2gh
A√2gh(1+1h)B√(1+12gh)nC√n2ghD√1+h2ghA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
 A√2ghBη√2ghC√2gh(1+1η)D√2gh(1−1η)
A√2ghBη√2ghC√2gh(1+1η)D√2gh(1−1η)
A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
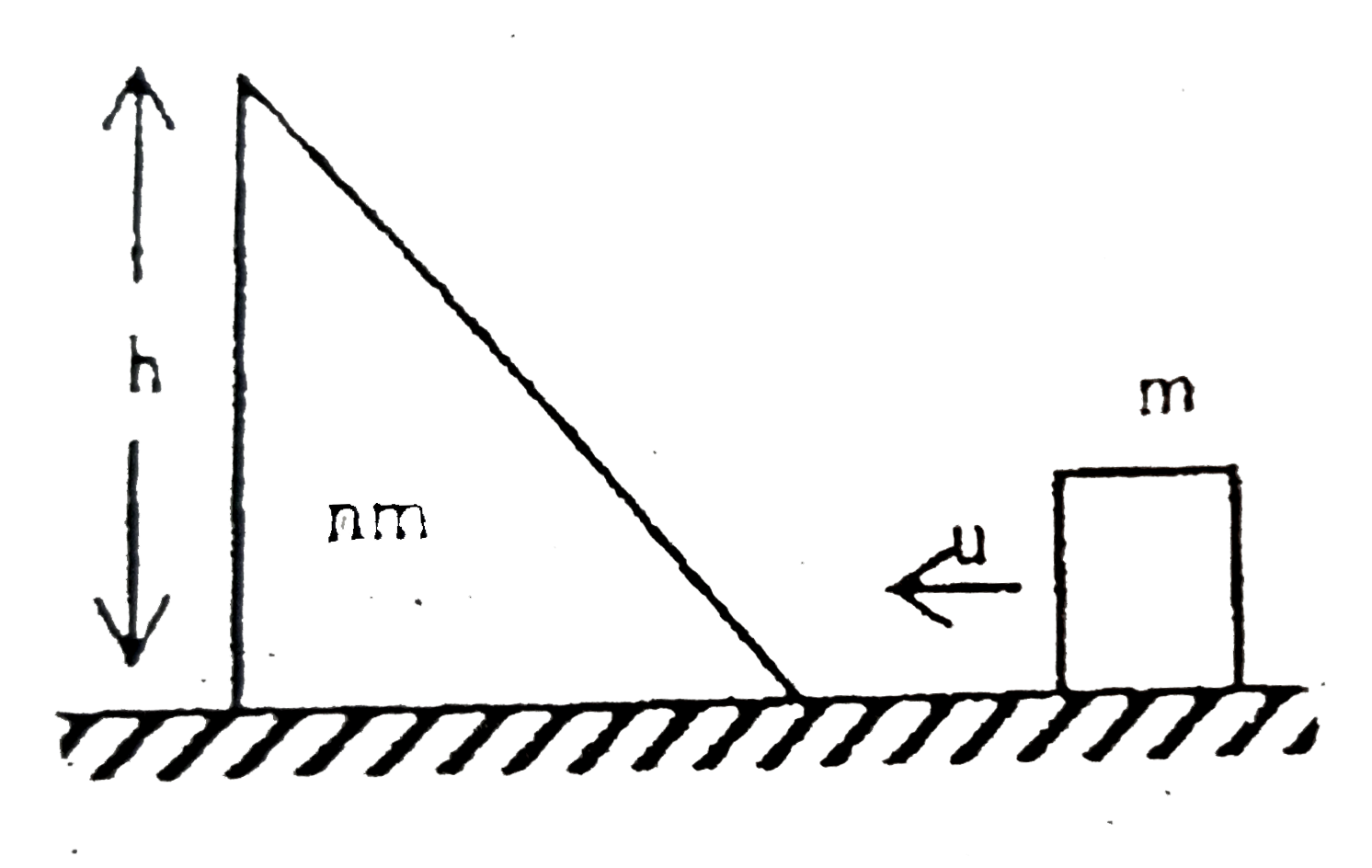
View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is

View Solution