A trolley moves in horizontal direction with an acceleration a. A simple pendulum of length l is suspended from the roof of the trolley. The time period of the pendulum will be
infinity
zero
The correct Answer is:D
To find the time period of a simple pendulum suspended from a trolley that is accelerating horizontally, we can follow these steps:
1. Understanding the System:
- We have a trolley moving with horizontal acceleration a.
- A simple pendulum of length L is suspended from the roof of the trolley.
2. Identifying Forces:
- The pendulum experiences two accelerations:
- The gravitational acceleration g acting downwards.
- The pseudo force due to the trolley's acceleration a acting horizontally in the opposite direction of the trolley's motion.
3. Effective Gravitational Acceleration:
- The effective gravitational acceleration geffective can be found by considering the resultant of the two accelerations (since they are perpendicular to each other).
- Using the Pythagorean theorem, we have:
geffective=√g2+a2
4. Time Period of the Pendulum:
- The formula for the time period T of a simple pendulum is given by:
T=2π√Lgeffective
- Substituting geffective into the formula, we get:
T=2π√L√g2+a2
5. Final Expression:
- Simplifying further, we can express the time period as:
T=2π√L√g2+a2
Final Answer:
Thus, the time period of the pendulum is:
T=2π√L√a2+g2
- We have a trolley moving with horizontal acceleration a.
- A simple pendulum of length L is suspended from the roof of the trolley.
- The pendulum experiences two accelerations:
- The gravitational acceleration g acting downwards.
- The pseudo force due to the trolley's acceleration a acting horizontally in the opposite direction of the trolley's motion.
- The effective gravitational acceleration geffective can be found by considering the resultant of the two accelerations (since they are perpendicular to each other).
- Using the Pythagorean theorem, we have:
geffective=√g2+a2
- The formula for the time period T of a simple pendulum is given by:
T=2π√Lgeffective
- Substituting geffective into the formula, we get:
T=2π√L√g2+a2
- Simplifying further, we can express the time period as:
T=2π√L√g2+a2
Thus, the time period of the pendulum is:
T=2π√L√a2+g2
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - CHECK YOUR NEET VITALS25videos
OSCILLATIONS AND WAVES
- BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs43videos
OSCILLATIONS AND WAVES
- BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs43videos
OSCILLATIONS AND WAVES
- BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)37videos
MOTION OF SYSTEM OF PARTICLES AND RIGID BODY
- BOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ14videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
Find the period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination a.
View SolutionWhat is the time period of a simple pendulum if length of the pendulum is equal to the radius of Earth ?
View Solution
Knowledge Check
- Question 1 - Select One
Time period of simple pendulum is
AT=2π√lgBT=2π√glCT=√2πlgDT=12π√gl - Question 2 - Select One
The time period of a simple pendulum of infinte length is
AinfiniteB2π√R/gC2π√g/RD12π√R/g - Question 3 - Select One
An amplitue of a simple pendulum of a period 'T' and length 'L' is increased by 5%. The new period of that pendulum will be
AT8BT4CT2DT
A vehicle is moving on a circular path of radius R with constant speed √gR. A simple pendulum of length l hangs from the ceilling of the vehicle. The time period of oscillations of the pendulum is
View SolutionTime period of simple pendulum suspended from a metallic wire
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionThe l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
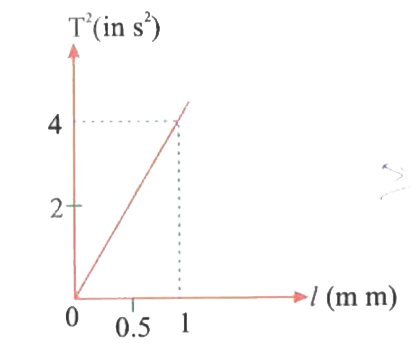 View Solution
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
View Solution

