A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is
Mω2L2
Mω2L
Mω2L4
Mω2L24
The correct Answer is:A
The force acting on the mass of liquid of length dx at a distance x from the axis of rotation O is as follows:

dF=(dm)×ω2
∴dF=MLdx×ω2. Therefore the force action at the other end is for the whole liquid in tube.
F∫L0MLω2xdx=MLω2∫L0xdx
=MLω2[x22]L=MLω2[L22−0]
=MLω22
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - LC_TYPE8videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - SCQ_TYPE29videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Knowledge Check
- Question 1 - Select One
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. Determine the force exerted by the liquid at the other end.
AMω2L2BMω2LCMω2L4DMω2L22
One end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?
 View Solution
View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
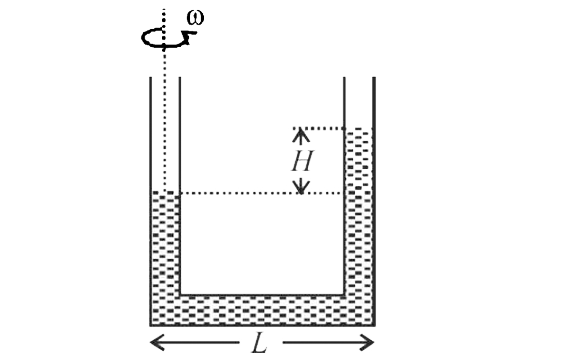 View Solution
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The graph of the pressure gradient (dPdx) with the distance x meaured from the axis of rotation is :View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View Solution
