A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
is zero
remains constant
goes on increasing
goes on decreasing
The correct Answer is:B
Angular momentum
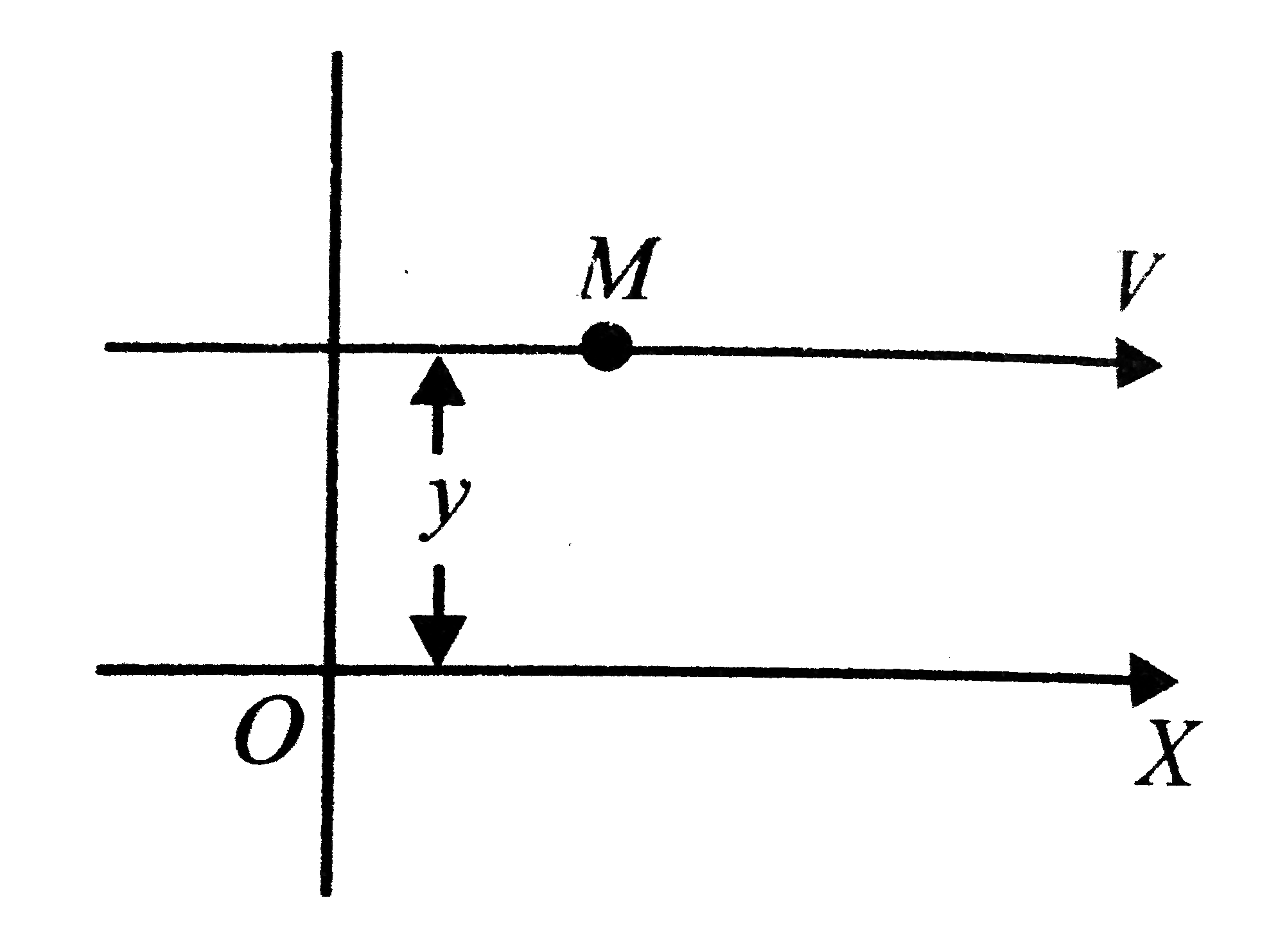
→L=→r×→p
L= momentum × perpendicular distance of line of action of momentum w.r.t point of rotation
L=Mv×y
The quantities on the right side of the equation are not changing. Thus, magnitude is constant.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - LC_TYPE8videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - SCQ_TYPE29videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionStatement - 1 : A particle moves with a constant velocity parallel to the x-axis. Its angular momentum w.r.t. the origin will remains constant.
Because
Statement - 2 : Angular momentum is defined as →L=→r×→PView SolutionA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
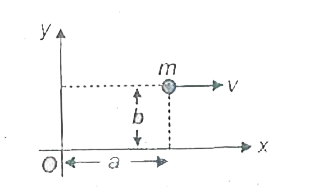
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
 View Solution
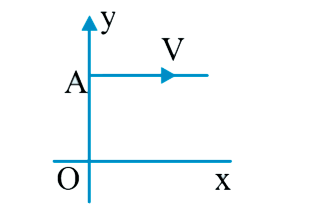
View SolutionA body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
 View Solution
View SolutionA particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)
 View Solution
View SolutionThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
View SolutionThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
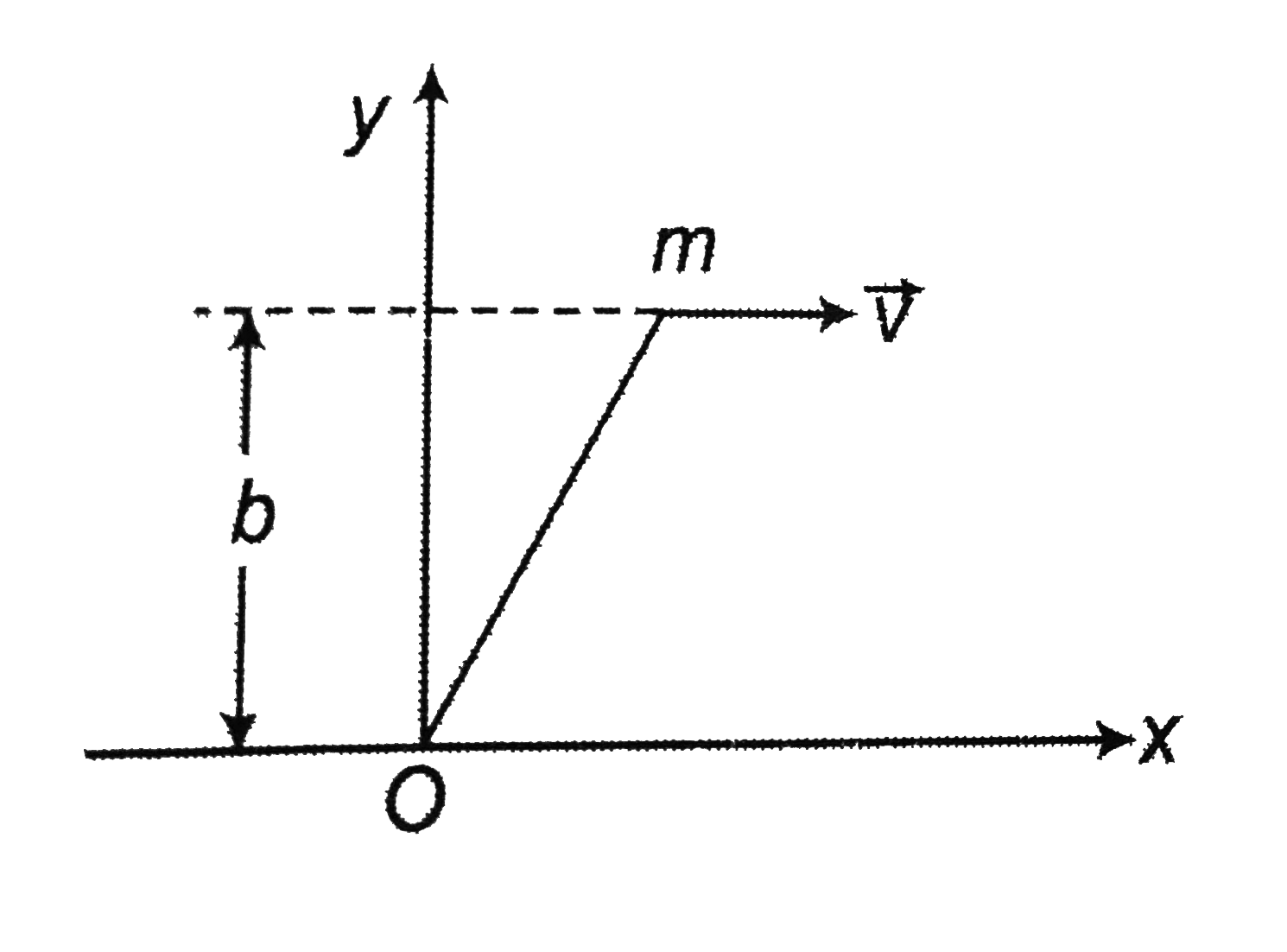
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.
 View Solution
View SolutionA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View Solution

