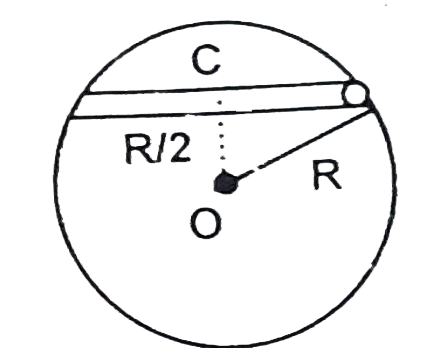
A tunnel is dug along a chord of non rotating earth at a distance d=R2 [R = radius of the earth] from its centre. A small block is released in the tunnel from the surface of the arth. The block comes to rest at the centre (C) of the tunnel. Assume that the friction coefficient between the block and the tunnel wall remains constant at μ.
![A tunnel is dug along a chord of non rotating earth at a distance d=(R)/(2) [R = radius of the earth] from its centre. A small block is released in the tunnel from the surface of the arth. The block comes to rest at the centre (C) of the tunnel. Assume that the friction coefficient between the block and the tunnel wall remains constant at mu. Calculate work done by the friction on the block. Calculate mu.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C07_E01_034_Q01.png) Calculate work done by the friction on the block. Calculate μ.
Calculate work done by the friction on the block. Calculate μ.
The correct Answer is:(a)−3gmM8R
√32
Step by step video, text & image solution for A tunnel is dug along a chord of non rotating earth at a distance d=(R)/(2) [R = radius of the earth] from its centre. A small block is released in the tunnel from the surface of the arth. The block comes to rest at the centre (C) of the tunnel. Assume that the friction coefficient between the block and the tunnel wall remains constant at mu. Calculate work done by the friction on the block. Calculate mu. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A tunnel is dug along a chord of Earth having length √3R is radius of Earth. A small block is released in the tunnel from the surfasce of Earth. The particle comes to rest at the centre of tunnel. Find coefficient of friction between the block and the surface of tunnel. Ignore the effect of rotation of Earth.
View SolutionA tunnel is dug along a chord of Earth having length √3R where R is radius of Earth. A small block is released in the tunnel from the surface of Earth. The particle comes to rest centre of tunnel. If the coefficient of friction between the block and the surface of tunnel is μ=2√3n, then find n. Ignore the effect of rotation of Earth.
View Solution
Knowledge Check
- Question 1 - Select One
A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
 A√3GM2RB√3GM4RC√3GM8RDd√3GM16R
A√3GM2RB√3GM4RC√3GM8RDd√3GM16R - Question 2 - Select One or More
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
A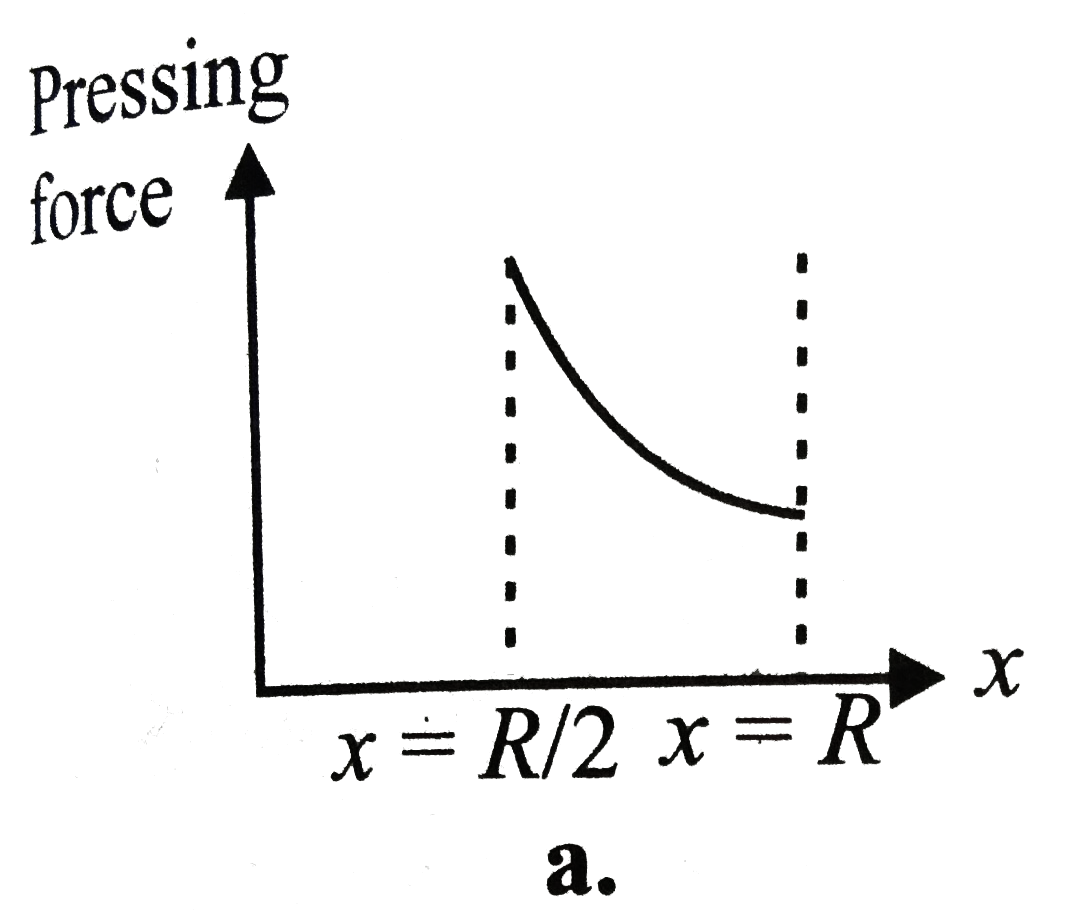 B
B C
C D
D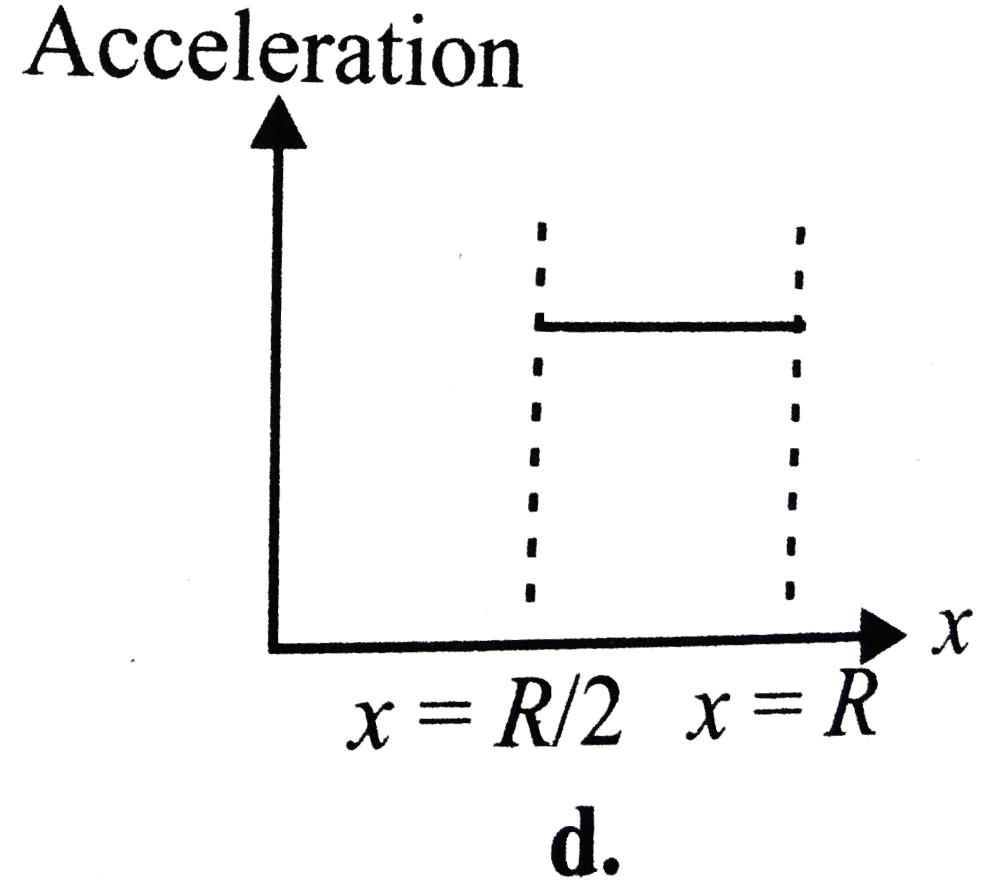
- Question 3 - Select One
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√Rg
What are tunnel proteins ?
View SolutionA tunnel ois dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionImagine a smooth tunnel along a chord of nonrotating earth at a distance R2 from the centre. R is the radius of the earth. A projectile is fired along the tunnel from the centre of the tunnel at a speed V∘=√gR [g is acceleration due to gravity at the surface of the earth]. (a) Is the angular momentum [about the centre of the earth] of the projectile onserved as it moves along the tunnel? (b) Calculate the maximum distance of the projectile from the centre of the earth during its course of motion.
View SolutionAssume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionA smooth tunnel is dug along the radius of the earth that ends at the centre. A ball is released from the surface of earth along the tunnel. If the coefficient of restitution is 0.2 between the surface and ball, then the distance travelled by the ball before second collision at the centre is
View Solution

