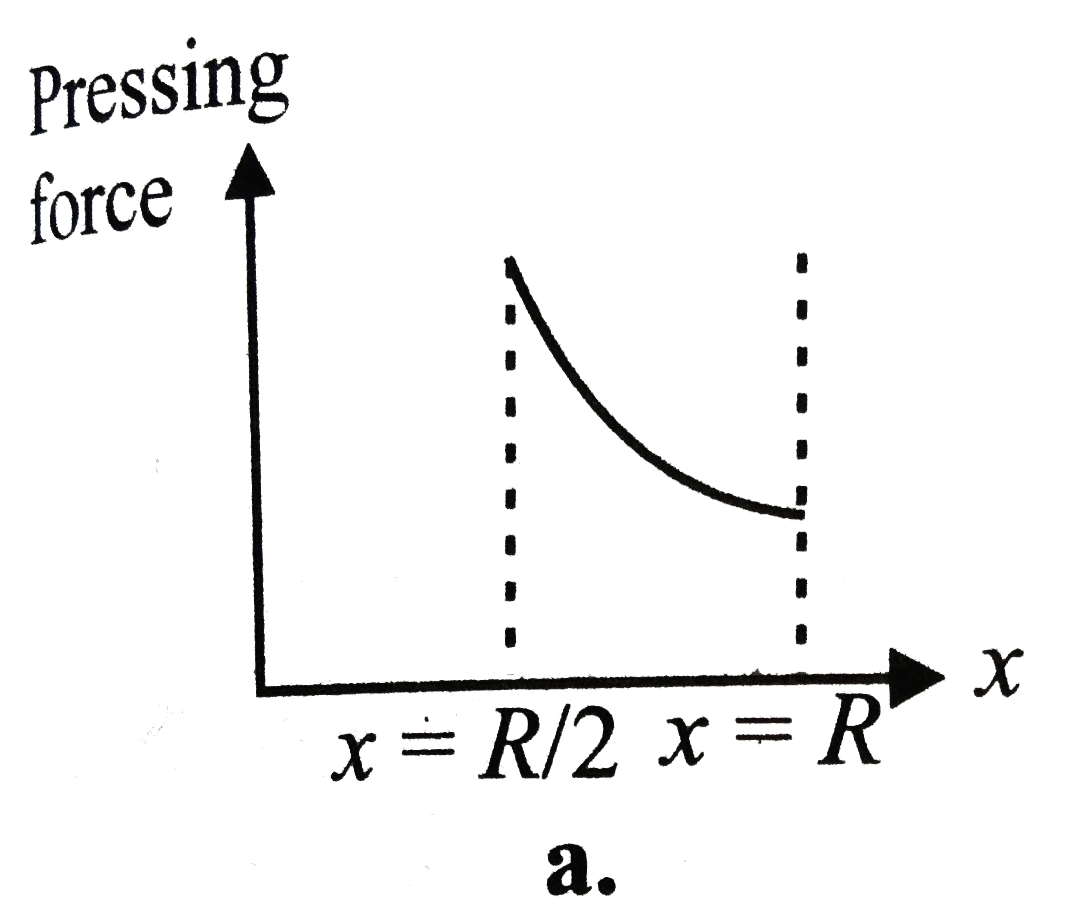
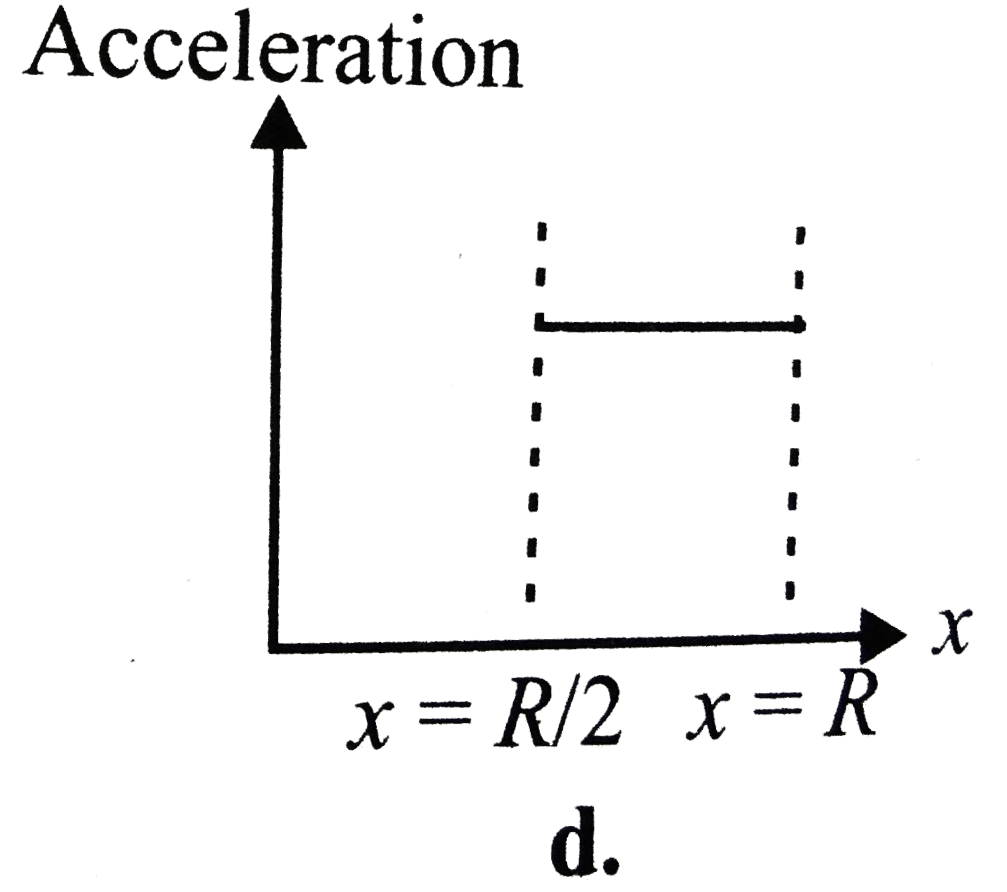
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to


The correct Answer is:B, C
To solve the problem, we need to analyze the situation of a particle released from one end of a frictionless tunnel dug along a chord of the Earth at a perpendicular distance of R/2 from the center of the Earth. We will derive the expressions for the pressing force by the particle on the wall of the tunnel and the acceleration of the particle as it moves through the tunnel.
Step 1: Understanding the Geometry
The tunnel is dug at a distance of R/2 from the center of the Earth. The distance of the particle from the center of the Earth is denoted as x. The gravitational force acting on the particle varies with depth, and we need to find expressions for the forces acting on the particle.
Step 2: Gravitational Force Inside the Earth
Inside the Earth, the gravitational force g′ at a distance x from the center can be given by:
g′=g(1−dR)
where d is the depth below the surface. Since the depth d can be expressed as R−x, we have:
g′=g(1−R−xR)=g(xR)
Step 3: Pressing Force on the Wall
The pressing force N exerted by the particle on the wall of the tunnel can be derived from the component of the gravitational force acting perpendicular to the wall. The angle θ can be determined from the geometry of the situation, where:
sinθ=R/2x
Thus, the normal force can be expressed as:
N=mg′sinθ
Substituting g′ and sinθ:
N=mg(xR)(R/2x)=mg2
This shows that the pressing force N is constant and does not depend on x.
Step 4: Acceleration of the Particle
The net force acting on the particle in the direction of the tunnel is given by:
F=mg′cosθ
Using g′=g(xR) and cosθ=√x2−(R/2)2x:
F=mg(xR)(√x2−(R/2)2x)=mg√x2−(R/2)2R
The acceleration a of the particle can be expressed as:
a=Fm=g√x2−(R/2)2R
Step 5: Analyzing the Acceleration Expression
The expression for acceleration shows that it varies with x and is zero when x=R/2. The acceleration is a parabolic function of x.
Conclusion
The pressing force by the particle on the wall of the tunnel is constant, while the acceleration of the particle varies parabolically with x. Therefore, the correct options for the graphs representing these relationships are:
- Pressing Force: Constant (Option B)
- Acceleration: Parabolic (Option C)
The tunnel is dug at a distance of R/2 from the center of the Earth. The distance of the particle from the center of the Earth is denoted as x. The gravitational force acting on the particle varies with depth, and we need to find expressions for the forces acting on the particle.
Inside the Earth, the gravitational force g′ at a distance x from the center can be given by:
g′=g(1−dR)
where d is the depth below the surface. Since the depth d can be expressed as R−x, we have:
g′=g(1−R−xR)=g(xR)
The pressing force N exerted by the particle on the wall of the tunnel can be derived from the component of the gravitational force acting perpendicular to the wall. The angle θ can be determined from the geometry of the situation, where:
sinθ=R/2x
Thus, the normal force can be expressed as:
N=mg′sinθ
Substituting g′ and sinθ:
N=mg(xR)(R/2x)=mg2
This shows that the pressing force N is constant and does not depend on x.
The net force acting on the particle in the direction of the tunnel is given by:
F=mg′cosθ
Using g′=g(xR) and cosθ=√x2−(R/2)2x:
F=mg(xR)(√x2−(R/2)2x)=mg√x2−(R/2)2R
The acceleration a of the particle can be expressed as:
a=Fm=g√x2−(R/2)2R
The expression for acceleration shows that it varies with x and is zero when x=R/2. The acceleration is a parabolic function of x.
The pressing force by the particle on the wall of the tunnel is constant, while the acceleration of the particle varies parabolically with x. Therefore, the correct options for the graphs representing these relationships are:
- Pressing Force: Constant (Option B)
- Acceleration: Parabolic (Option C)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct24videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning13videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Subjective15videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
A tunnel ois dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionAssume that a tunnel is dug along a cord of earth at a perpendicular distance R2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
View Solution
Knowledge Check
- Question 1 - Select One
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√Rg - Question 2 - Select One
A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
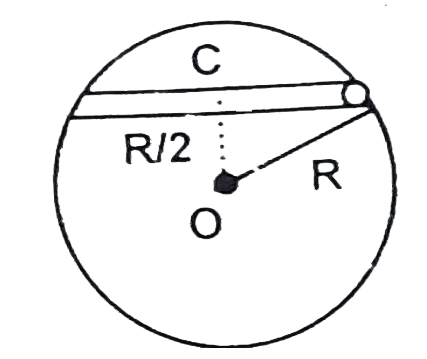 A√3GM2RB√3GM4RC√3GM8RDd√3GM16R
A√3GM2RB√3GM4RC√3GM8RDd√3GM16R - Question 3 - Select One
If a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle isA√2GMRB√GMRC√3GM2RD√GM2R
(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre.
(b) A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.View SolutionAssume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal toView Solution

