A ring having non-uniform distribution of mass M and radius R is being considered. A point mass m0 is taken slowly towards the ring. In doing so, work done by the external force against the gravitational force exerted by ring is

GMm0√2R
GMm0R[1√2−1√5]
GMm0R[1√5−1√2]
It is not possible to find the required work as the nature of distribution of mass is not known.
The correct Answer is:B
Even though the distribution of the mass is unknown, we can find the potential due to the ring on any axial point because from any axial point the entire mass is at the same distance (whatever woud be the nature of distribution).
Potential at A due to the ring is VA=GM√(2R)
Potential at B due to the ring is VB=GM√5R
dU=Uf−Ui−Ui=UB−UA=m0(VB−VA)
GMm0R[−1√5+1√2]
Wgr=−Wext
Wgr=dU=−Wext
Wext=dU=GMm0R[1√2−1√5]
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Find the moment of inertia of uniform ring of mass M and radius R about a diameter.
View SolutionA uniform ring of mass 2m and radius a is placed directly above the uniform sphere of mass M and of same radius. The centre of ring is at distance √3a from the centre of sphere. The gravitational force exerted by the sphere on the ring is NGMma2 units. Calculate is the value of N?
View Solution
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRThe total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2A ring of mass m1 and radius R is fixed in space at some location. An external agent brings a point mass m2 from infinity to centre of the ring. Work done by the external agent will be
A−Gm1m2RBGm1m2RCG√m21+m22RDGm1m2R(m21+m22)
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
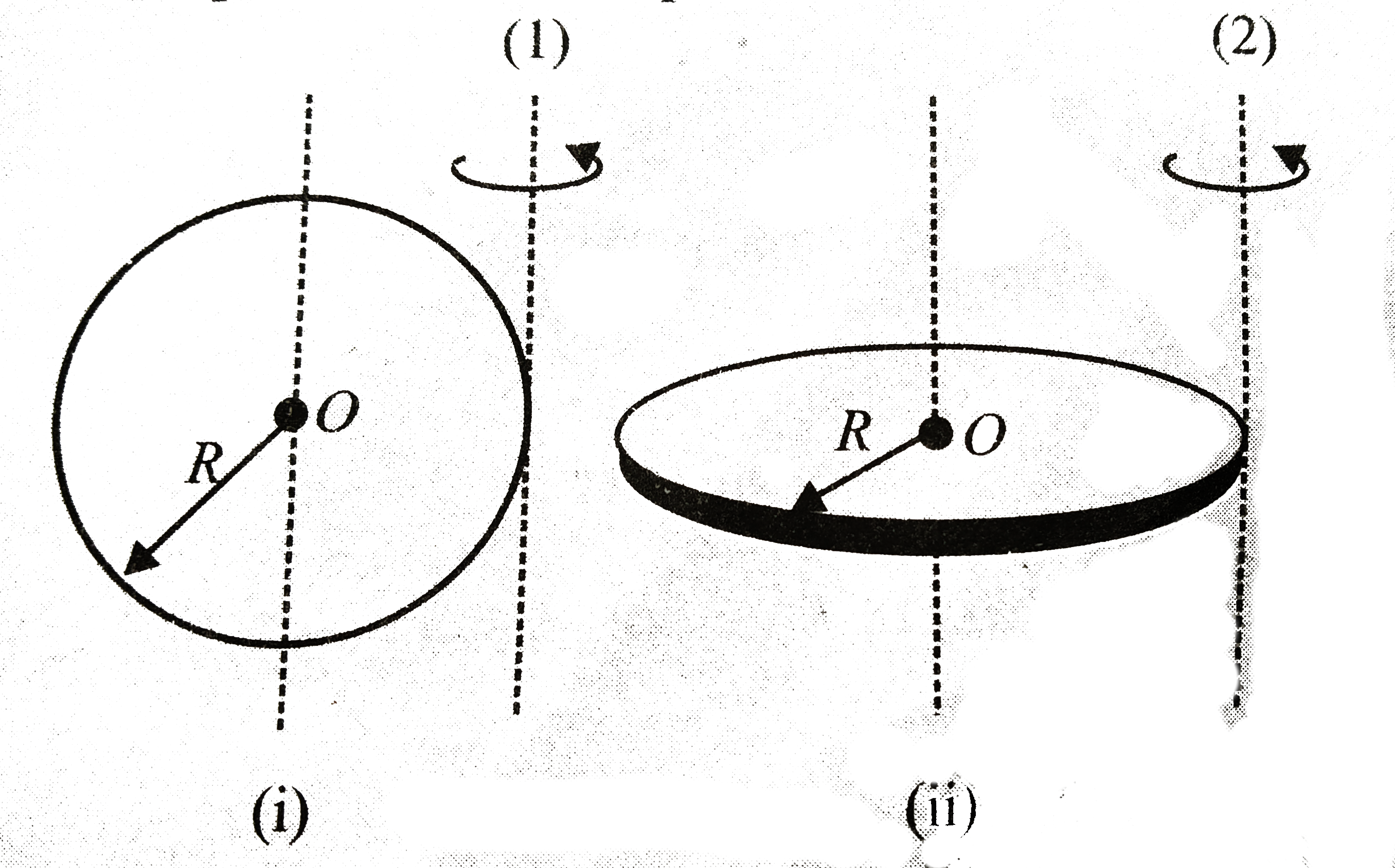
View SolutionA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
View Solution
