(a) Two monochromatic waves emanating from two coherent sources have the displacements represented by
y1=acosωt
and y2=acos(ωt+ϕ),
where ϕ is the phase difference between the two displacements . Show that the resultant intensity at a point due to their superposition is given by I=4I0cos2ϕ/2, where I0=a2.
(b) Hence obtain the conditions for constructive and destructive interference.
(a) The resultant displacement is given by :
y=y1+y2
=acosωt+acos(ωt+ϕ)
=acosωt(1+cosϕ)−asinωtsinϕ
Put Rcosθ=a(1+cosϕ)
Rsinθ=asinϕ
∴R2=a2(1+cos2ϕ+2cosϕ)+a2sin2ϕ
=2a2(1+cosϕ)=4a2cos2.ϕ2
∴I=R24a2cos2.ϕ2=4I0cos2.ϕ2
For constructive interference,
cos.ϕ2=±1 or ϕ2=nπ or ϕ=2nπ
For destructive interference
cos.ϕ2=0 or ϕ2=(2n+1).π2 or ϕ=(2n+1)π
Topper's Solved these Questions
- WAVE OPTICSBOOK - OSWAAL PUBLICATIONCHAPTER - WAVE OPTICSEXERCISE - Topic 2 INTERFERENCE (short answer type question-II )
1 Videos
- WAVE OPTICSBOOK - OSWAAL PUBLICATIONCHAPTER - WAVE OPTICSEXERCISE - Topic 2 INTERFERENCE (long answer type question )
4 Videos
- WAVE OPTICSBOOK - OSWAAL PUBLICATIONCHAPTER - WAVE OPTICSEXERCISE - Topic 2 INTERFERENCE (very short answer )
3 Videos
- SOLVED PAPER 1BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER 1EXERCISE - Exercise
39 Videos
Similar Questions
(a) (i) Two independent mono chromatic sources of light cannot produced a sustained interference pattern'. Give reason.
(ii) Light waves each of amplitude ''a'' and frequency ''w'', emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given byy3=acosωtandy2=acos(ωt+ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View SolutionConsider two coherent sources S1andS2 producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by S1 be given by
and the displacement by S2 be Y1=acosωt
Y2=acos(ωt−ϕ)
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
I=4a2cos2ϕ/2
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
∠i+∠e=∠A+∠δ
Where δ and e denote the angle of deviation and angle of emergence respectively.
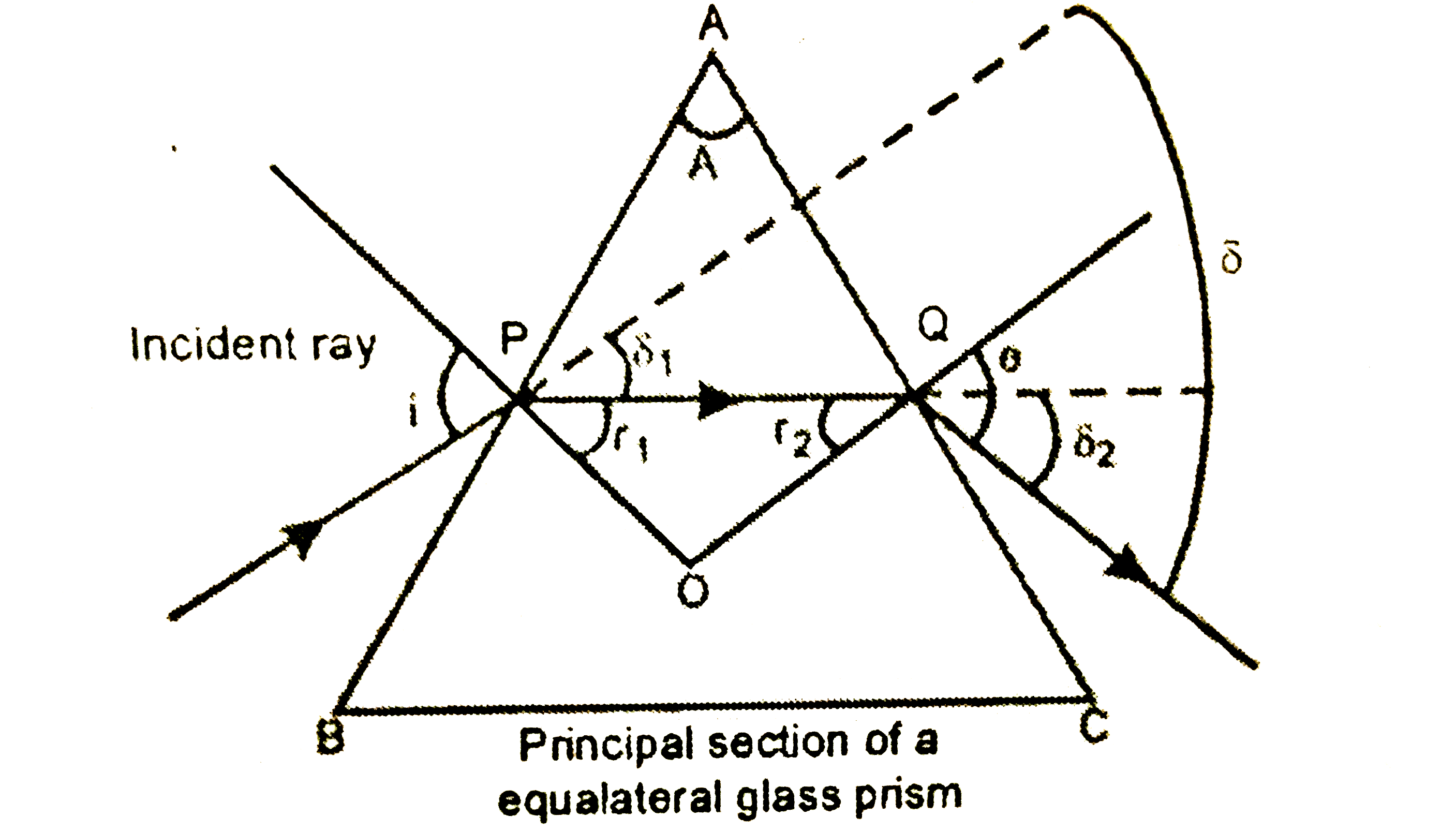
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (μ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm) . Hence obtain the value of the refractive index for angle Ae=60∘ .
View Solution
Knowledge Check
The two waves represented by y1=asin(ωt) and y2=bcos(ωt) have a phase difference of
A(a) 0B(b) π2C(c) πD(d) π4Two waves are represented by the equations y1=asin(ωt=kx+0.57)m and y2=acos(ωt+kx)m where x is in metre and t in second. The phase difference between them is
A1.25radB1.57radC0.57radD1.0radTwo waves are represented by the equations
y1=asin(ωt+kx+0.57)m and
y2=acos(ωt+kx)m,
where x is in metres and t is in seconds. The phase difference between them isA1.0 radianB1.25 radianC1.57 radianD0.57 radian
(a) (i) 'Two independent monochromatic sources light cannot produce a sustained interference pattern.' Give reasons.
(ii) Light waves each of amplitude "a" and freuency "ω", emanating from two coherent light sources superpose at a point. If the displacement due to these waves is given by y1=acosωtandy2=acos(ωt+ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double-slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View Solution(a) (i) Two independent mono chromatic sources of light cannot produced a sustained interference pattern'. Give reason.
(ii) Light waves each of amplitude ''a'' and frequency ''w'', emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given byy3=acosωtandy2=acos(ωt+ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View Solution(a) (i) Two independent mono chromatic sources of light cannot produced a sustained interference pattern'. Give reason.
(ii) Light waves each of amplitude ''a'' and frequency ''w'', emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given byy3=acosωtandy2=acos(ωt+ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
View SolutionTwo waves are represented by the equations
y1=asin(ωt+kx+0.57)m and
y2=acos(ωt+kx)m,
where x is in metres and t is in seconds. The phase difference between them is
View SolutionThe equation of the displacement of two particles making SHM are represented by y1=asin(ωt+ϕ)&y2−acos(ωt). Phase difference between velocities of two particles is
View Solution
