A uniform ball of radius R rolls without slipping between the rails such that the horizontal distance is √3R between the two contact points of te rails of the ball. Figure (a) shows front view of the ball and figure (b) shows the side view of the ball. vCM is the velocity of centre of mass of the ball and ω is the angular velocity of the ball after rolling down a distance 2h along the incline then 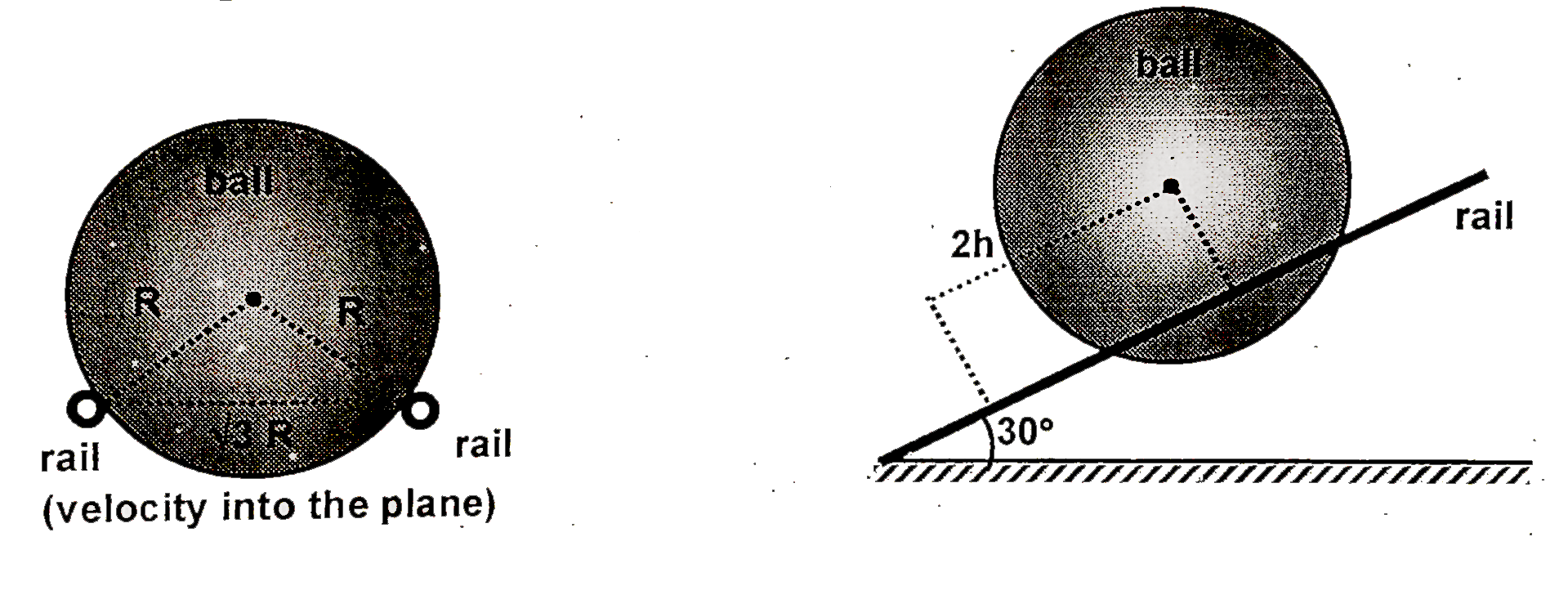
VCM=ωR
VCM=ωR2
VCM=√10gh13
VCM=√10gh7
The correct Answer is:B, C
vCM=ω√R2−3R24=ωR2 (from pure rolling)
mgh=12mv2cm+1225mR2ω2 (from conservation of energy)
∴vCM=√10gh13
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionGregory rolls a plastic ball on the floor. The ball stops after rolling a certain distance. The ball stops because of the presence of
View Solution
Knowledge Check
A ball is rolling without slipping in a spherical shallow bowl (radius R) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, the period of oscillation
 Aincreases slightlyBis reduced by a factor of 1/2Cis increased by a factor of 2Ddecreases slightly
Aincreases slightlyBis reduced by a factor of 1/2Cis increased by a factor of 2Ddecreases slightlyA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
A√gRB√5gRC√10gRD√3gRA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K, If radius of the ball be R, then the fraction of total energy associated with its rotational energy will be
AK2K2+R2BR2K2+R2CK2+R2R2DK2R2
A ball is wbhirled ina circle by attaching it to a fixed point with a string. Is the an angular rotatioin of the ball about its centre? If yes, is this angular velocity equal to the angular velocity of the ball about the fixed point.
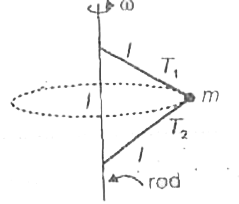
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionA spherical ball of radius r and mass m is rolling without slipping on a horizontal table. Calculate the percentage of KE, which is translational.
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
View SolutionA ball rolls without slipping. The radius of gyration of the ball about about an axis passing through its center of mass is K. If radius of the ball be R, then the fraction of total energy associated with its rotational energy be
View Solution
