In the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
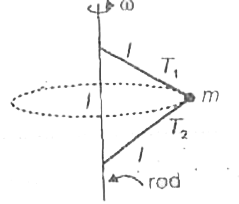
T1>T2
T2>T1
T1=T2
T1=T26
Step by step video & image solution for In the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity omega_(1) when by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
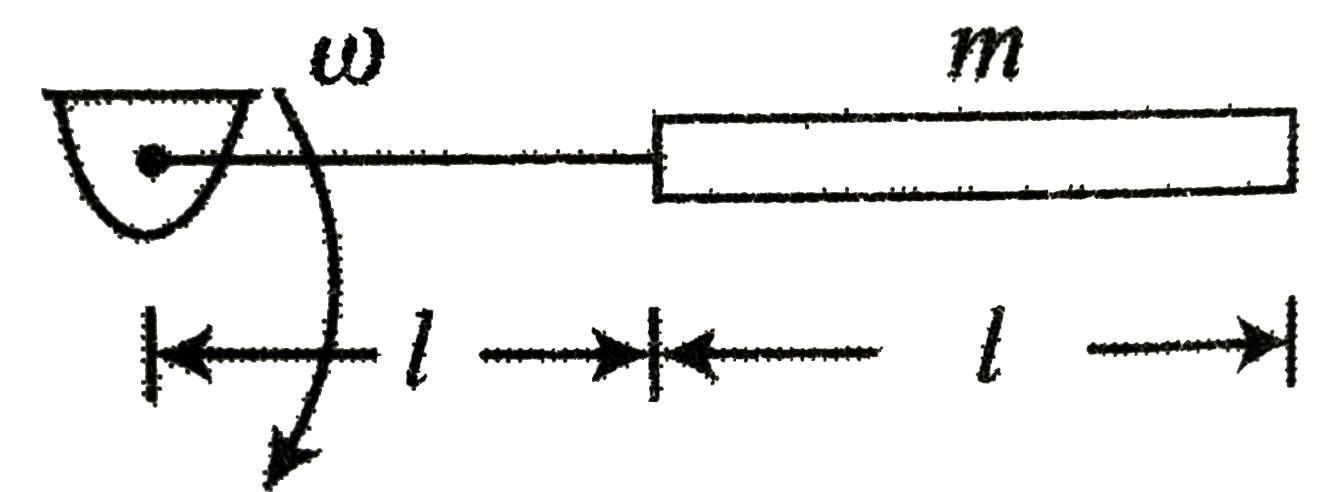
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionIf the rod were translating as well as rotating, what will be its emf? Assume that the centre of mass has a velocity v and the rod is rotating with an angular velocity ω atout its centre of mass.
View Solution
Knowledge Check
A disc of radius R has a light pole fixed perpendicular to the disc at its periphery whish in turn has a pendulum of legth R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is
 A(√3gR)1/2B(√3g2R)1/2C(g√3R)1/2D⎛⎜ ⎜⎝√2g(√2+1)R⎞⎟ ⎟⎠1/2
A(√3gR)1/2B(√3g2R)1/2C(g√3R)1/2D⎛⎜ ⎜⎝√2g(√2+1)R⎞⎟ ⎟⎠1/2A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 Aω0BMω0M+12mCMω0M+2mDMω0M+6m
Aω0BMω0M+12mCMω0M+2mDMω0M+6m
Three balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
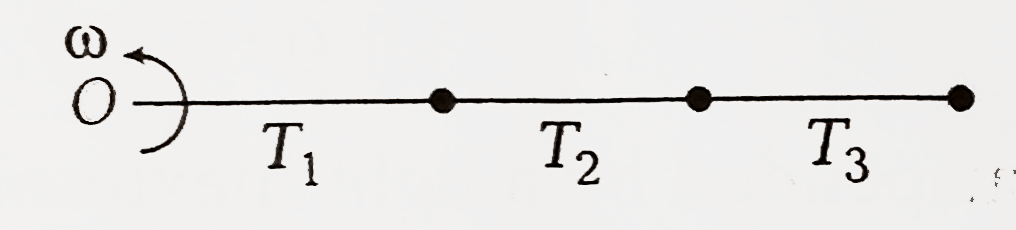
View SolutionThe figure shows a rod arranged at an angle of 30∘ from the horizontal. Two strings are fixed to rod as shown. Attached to the two strings is the mass m as shown. The rod is rotated maintaining its direction in space, so that m travels in a circular path. The strings are of equal length and make angle of 60∘ with the rod as shown. Calculate the minimum value of the tangential speed (ms) of the mass such that the string with tension T2 does not become slack when the mass is directly aboye the rod. Take length of string as. l=2.4m
'(##CEN_KSR_PHY_JEE_C07_036_Q22##)'
View SolutionA midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO′ as shown in figure. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO′ and to the end.

View Solution
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0. Change in the rotational kinetic energy of the system is
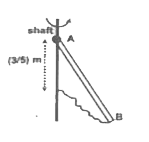
View SolutionA rod AB of length l = 1m and mass m = 2kg is pinned to a vertical shaft and a massless string is tied with the shaft at the lower end of the rod ( length of the string is 45m ) as shown in figure.If the shaft starts rotating with a constant angular velocity ω=5 rad / sec. Then find the tension in the string.
View Solution
