A uniform bar of length I and mass m stands vertically touching a vertical wall (y-axis). When slightly displaced, its lower end begins to slide along the floor (x-axis). Obtain an expression for the angular velocity (ω) of the bar as a function of O. Neglect friction everywhere.

The correct Answer is:√3g(1−sinθ)l)
The position of instantaneous axis of rotation (IAOR) is shown in figure.
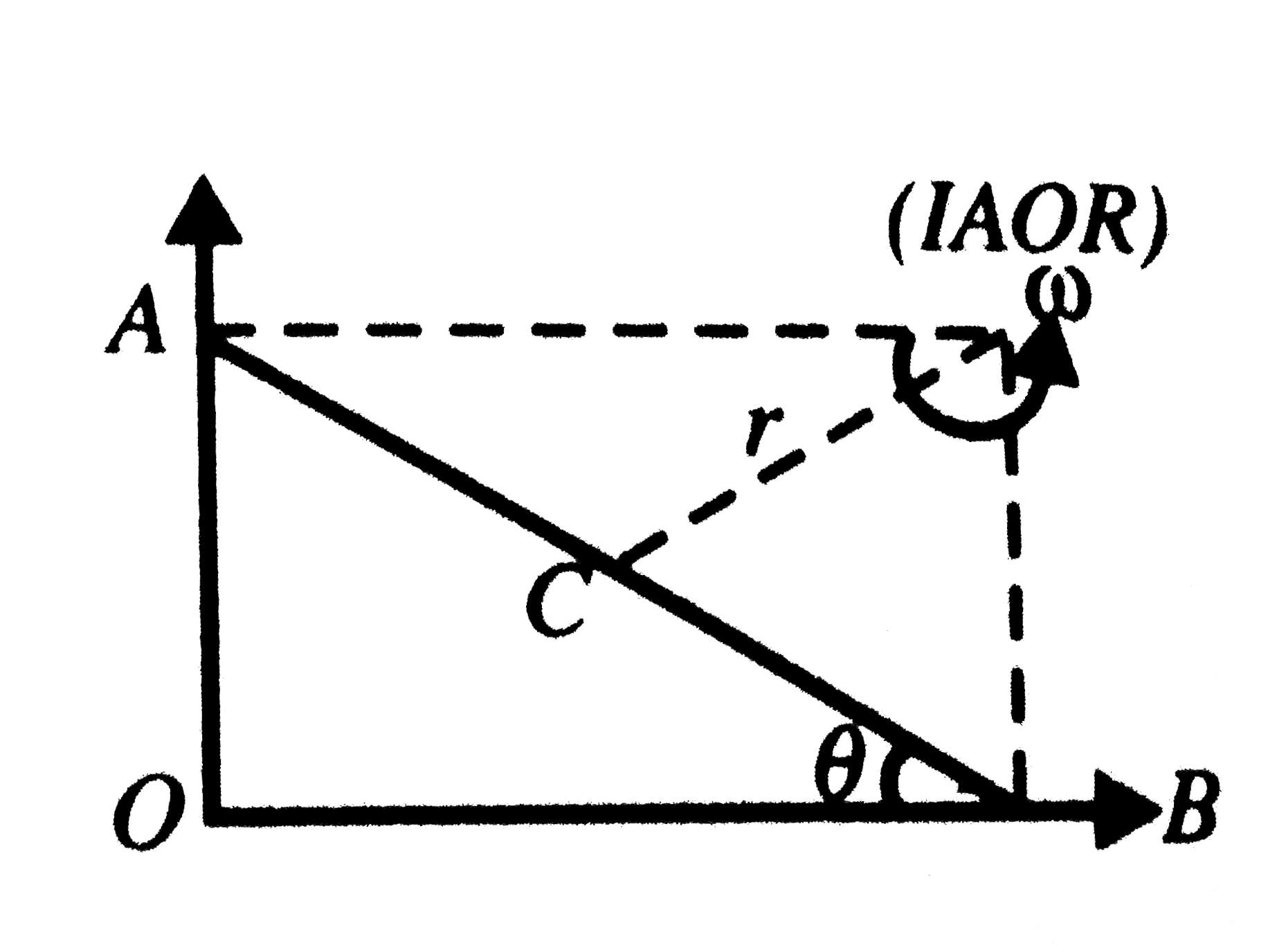
C=(l2cosθ,l2sinθ)
r=l2= half of the diagonal
All surfaces are smooth. Therefore, mechanical energy will remain conserved.
∴ Decrease in gravitational potential energy of bar = increae in rotational kinetic energy of bar about IAOR.
∴mgl2(1−sinθ)=12Iω2 .....i
Here I=ml212+mr2 (about IAOR)
or I=ml212+ml24=ml23
Substituting in eqn i we have
mgl2(1−sinθ)=12(ml23)ω2
or ω=√3g(1−sinθ)l
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.
View Solution
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
View Solution
Knowledge Check
A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
A13l2ω2gB16lωgC12l2ω2gD16l2ω2gA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its cenre of mass rises to a maximum height of :
A1lω6gB1l2ω2gC1l2ω26gD1l2ω23gA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
A√2glB√3glC√5glD√mgl
A conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA uniform rod of length l is held vertically on a horizontal floor fixing its lower end, the rod is allowed to fall onto the ground. Find (i) its angular velocity at that instant of reaching the ground (ii) The linear velocity with which the tip of rod hits the floor.
View SolutionA uniform thin rod of mass m and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbane at t = 0 causes the lower end t slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centr of mass of the rod during its fall?
(ii) Find the equaiton to the trajectory of a point on the rod shape of the path of this point?
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View Solution
