A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be regarded as uniform.
Step by step video & image solution for A uniform disc of radius R is spinned to the angular velocity omega and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be regarded as uniform. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question30videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Conceptual MCQs Single Option Correct39videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem81videos
NEWTONS LAWS OF MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
Similar Questions
A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be neglected as uniform.
View SolutionA uniform disc of radius r0 lies on a smooth horizontal plane. A similar disc spinning with the angular velocity ω0 is carefully lowered onto the first disc. How soon do both discs spin with the same angular-velocity if the friction coefficient between them is equal to μ?
View Solution
Knowledge Check
- Question 1 - Select One
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg - Question 2 - Select One or More
A disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are
 Athe time until rolling beginsBthe displacement of the disc until rolling beginsCthe velocity when rolling beginsDthe work done by the force of friction
Athe time until rolling beginsBthe displacement of the disc until rolling beginsCthe velocity when rolling beginsDthe work done by the force of friction - Question 3 - Select One
A uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point
View SolutionA disc is undergoing rolling on a horizontal surface. Which of the statement about angular momentum of the disc is incorrect ?
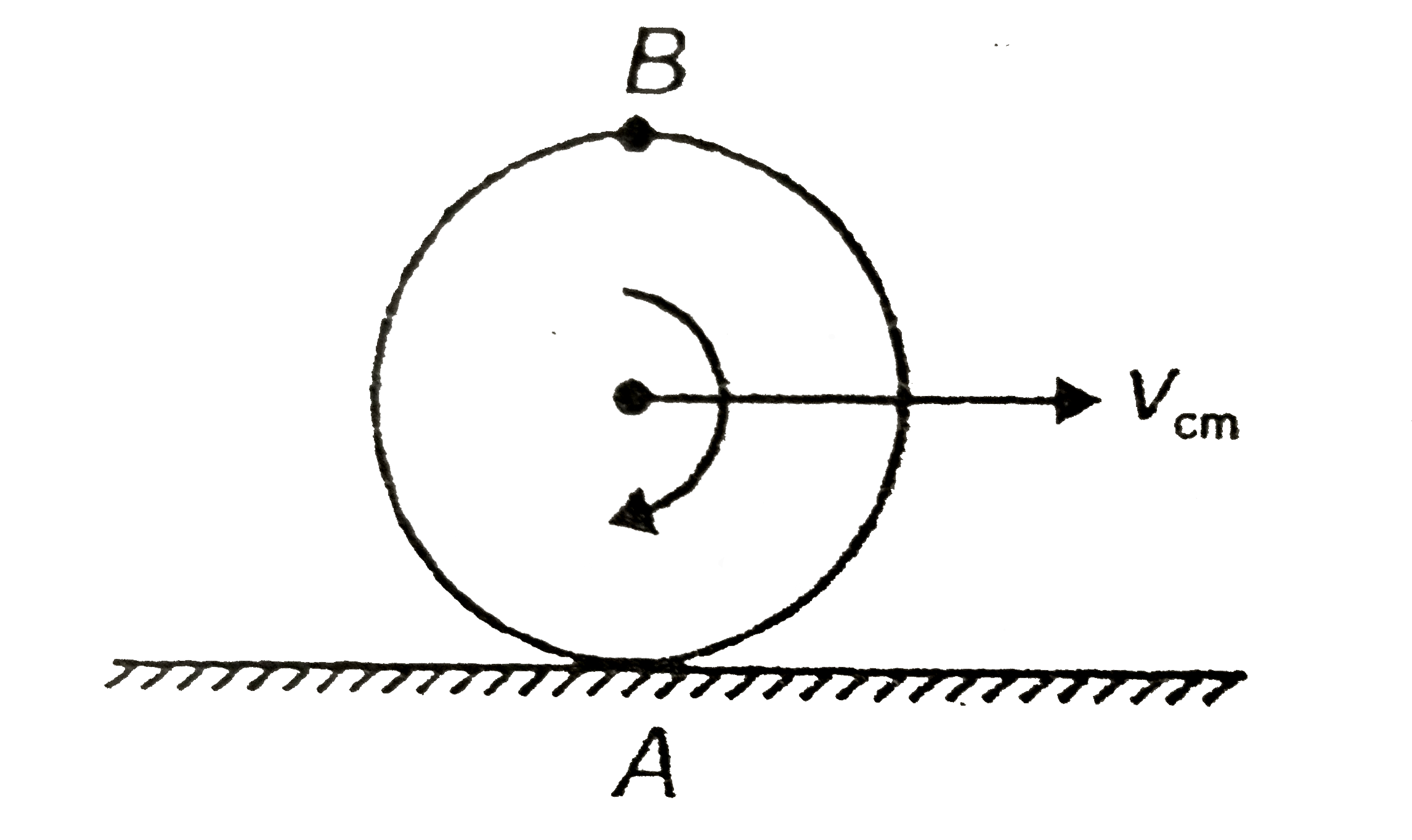 View Solution
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionWe have a disc of neglligible thickness and whose surface mass density varies as radial distance from centre as σ=σ0(1+rR), where R is the radius of the disc. Specific heat of the material of the disc isC.
Disc is given an angular velocity ω0 and placed on a horizontal rough surface such that the plane of the disc is parallel to the surface. Coefficient of friction between disc and suface is μ. The temperature of the disc is T0.
Answer the following question on the base of information provided in the above paragraph
If the kinetic energy lost due to the friction between disc and surface is absorbed by the disc the moment heat is generated, by the mass lying at the point where the energy is lost. Assume that there is no radial heat flow in betwen disc particles. Rate of change in temperature at a point lying at r distance away from centre with time, before disc stops rotating, will be (α-magnitude of angular acceleration of rod)View SolutionWe have a disc of neglligible thickness and whose surface mass density varies as radial disance from centre as σ=σ0(1+rR), where R is the radius of the disc. Specific heat of the material of the disc isC.
Disc is given an angular velocity ω0 and placed on a horizontal rough surface such that the plane of the disc is parallel to the surface. Coefficient of friction between disc and suface is μ. The temperature of the disc is T0.
Answer the following question on the base of information provided in the above paragraph
Magnitude of angular acceleration of disc isView Solution

