A uniform magnetic field B exists in a cylindrical region, shown dotted in. The magnetic field increases at a constant rate dBdt Consider a circle of radius r coaxial with the cylindrical region. (a) find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of hte square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part(a).
 Solution in Gujrati
Solution in Gujrati
(a) work done per unit per unit test change is <br>phi.E.dl=e implies E phi .dl=(d phi)/(dt)implies E. 2 pi r =(dB)/(dt)xxA<br>implies E 2 pi r = pi r^2(dB)/(dt)<br>implies E= (pi r^2)/(2 pi r) (dB)/(dt) =(r/2)(dB)/(dt)<br>(b)whenthe□isconsred,
phi.e.dt=e<br>implies Exx2rxx4=(dB)/(dt)(2r)^2<br>implies E = (dB)/(dt) ((4r^2)/(8r)<br> impliesE=(r/2) (dB)/(dt). <br>(c) the electric field at the point has the same value as (a).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
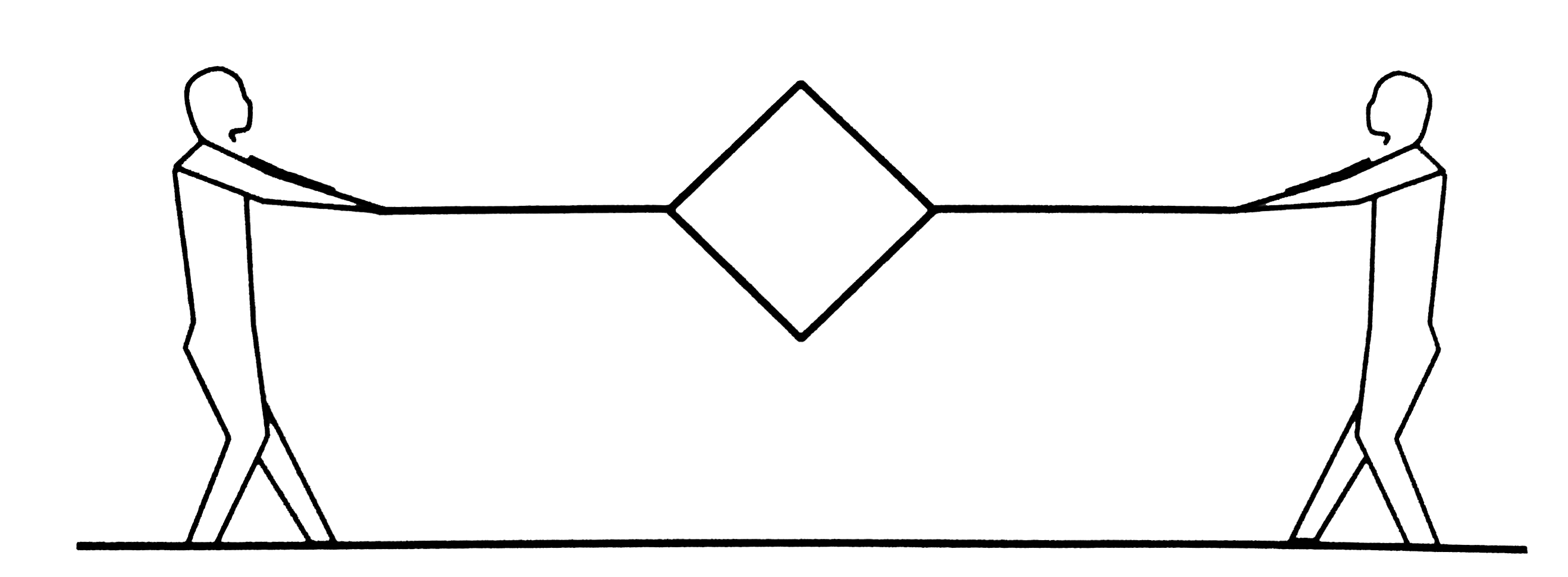
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
View SolutionA uniform magnetic field B exists in a cylindrical region of radius I0cm as shown in figure. A uniform wire or length 80cm and resistance 44.0Omega is bent into a square frame and is placed with one side along a diameter of the cylindrical region. if the magnetic field increases at a constant rate of 0.0I0T//sec , the current induced in the frame
View SolutionA time varying magnetic field B = Kr^(3)t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at r (R )/(2) is
View SolutionA uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
View SolutionA uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
View SolutionThe value of the magnetic field in a cylindrical region (dB)/(dt)=0.05 Tesla increases at the rate of seconds / second as shown in the figure. The radius of the cylindrical sphere is R = 3 cm. A concentric ring of radius r is placed in this region. The direction of the induced electric field at the place of the ring is
View SolutionThe value of the magnetic field in a cylindrical region (dB)/(dt)=0.05 Tesla increases at the rate of seconds / second as shown in the figure. The radius of the cylindrical sphere is R = 3 cm. A concentric ring of radius r is placed in this region. Inspired viva between point A and B. Force is
View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
View Solution
