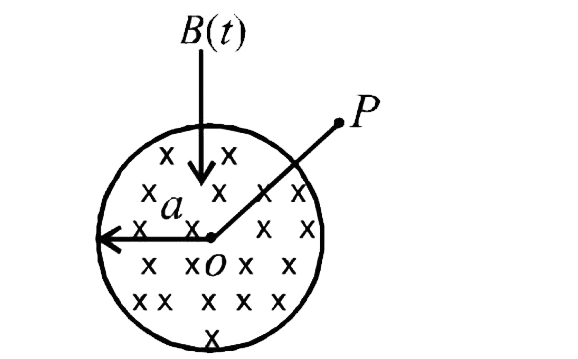
A uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

a) is zero
b) decreases as 1r
c) increases as r
d) decreases as 1r2
∫E.d1=∣∣∣dϕdt∣∣∣=S∣∣∣dBdt∣∣∣ or E(2πr)=πa2∣∣∣dBdt∣∣∣
For r≥a
∴E=a22r∣∣∣dBdt∣∣∣
∴ Induced electic field ∝1/r
For r≤a
E(2πr)=πr2∣∣∣dBdt∣∣∣orE=r2∣∣∣dBdt∣∣∣ or E∝r
At r=a,E=a2∣∣∣dBdt∣∣∣
Therefore variation of E with r (distance from centre) will be as follows
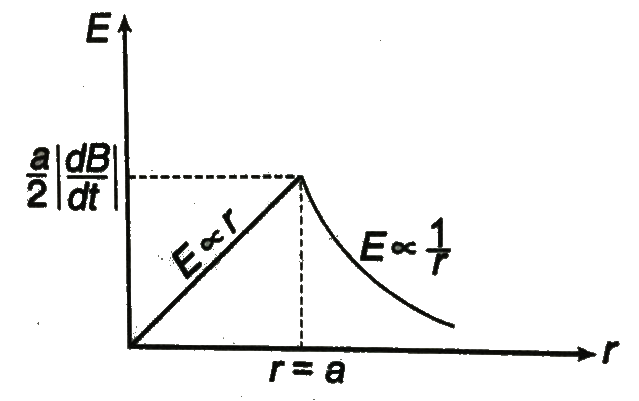
∴ The correct option is b
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 63videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Miscellaneous Examples5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 42videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 View Solution
View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
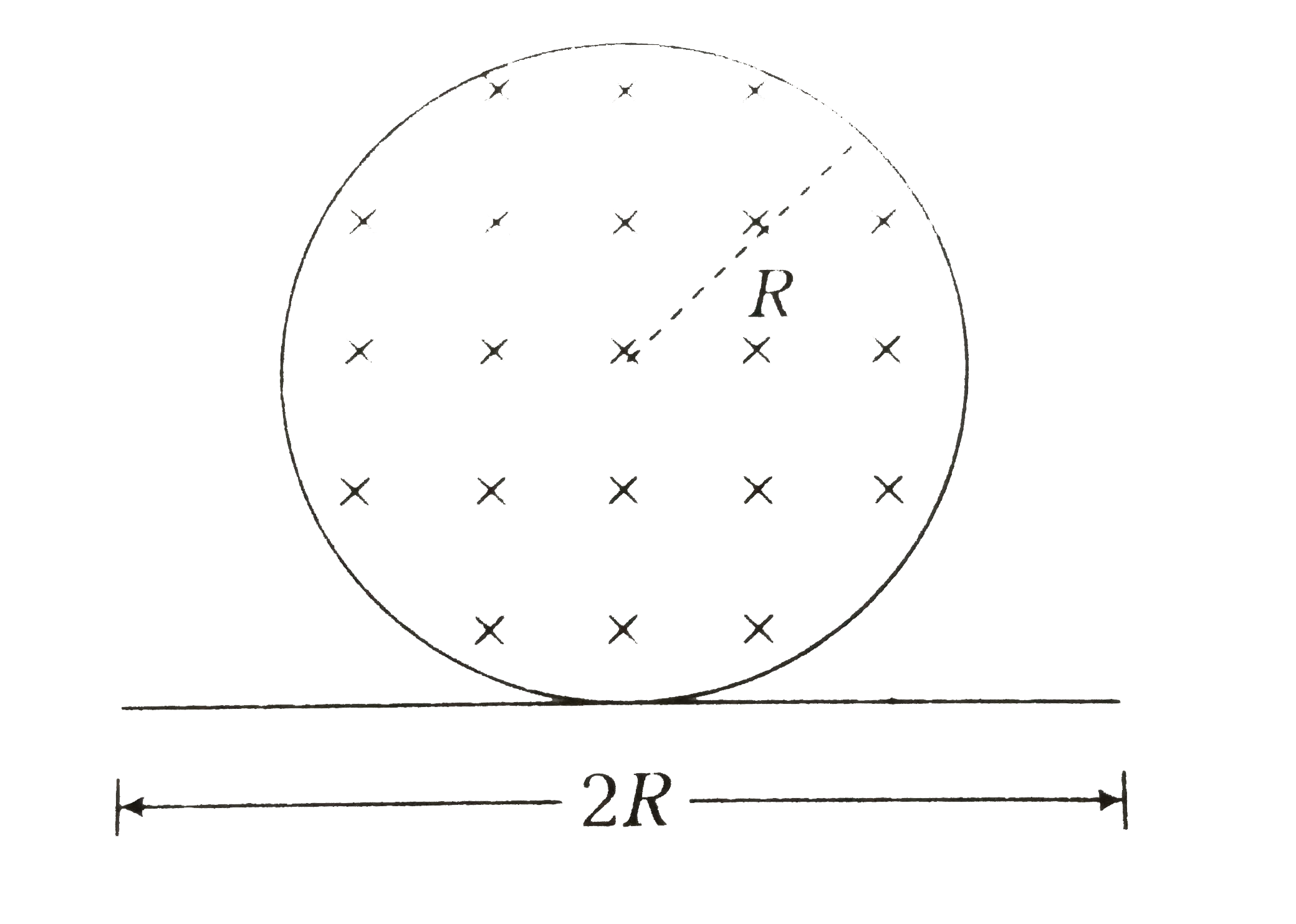
The magnitude of induced emf across the rod isView SolutionA uniform magnetic field exists in a circular region of radius R centred at O. The field is perpendicular to the plane of paper and is strength varies with time as B=B0t. Find the induced electric field at a distance r from the centre for (i)r<R, (ii) r>R. Also, plot a graph between |E| and r for both the cases.
View SolutionThe magnetic field in a certain cylindrical region is changing with time according to the law B=[16−4t2] Tesla . The magnitude of induced electric field at point P at time t= time =2 sec , is
 View Solution
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

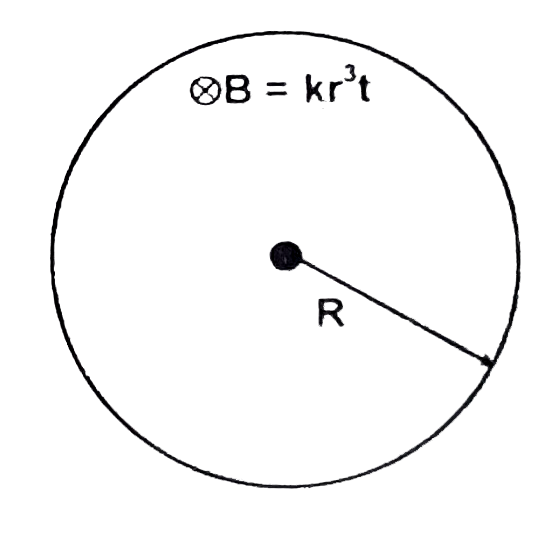
The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem isView SolutionA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
 View Solution
View SolutionA uniform but time varying magnetic field exists in cylindrical region and directed into the paper. If field decreases with time and a positive charge is placed at any point inside the region, then it moves :-
 View Solution
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

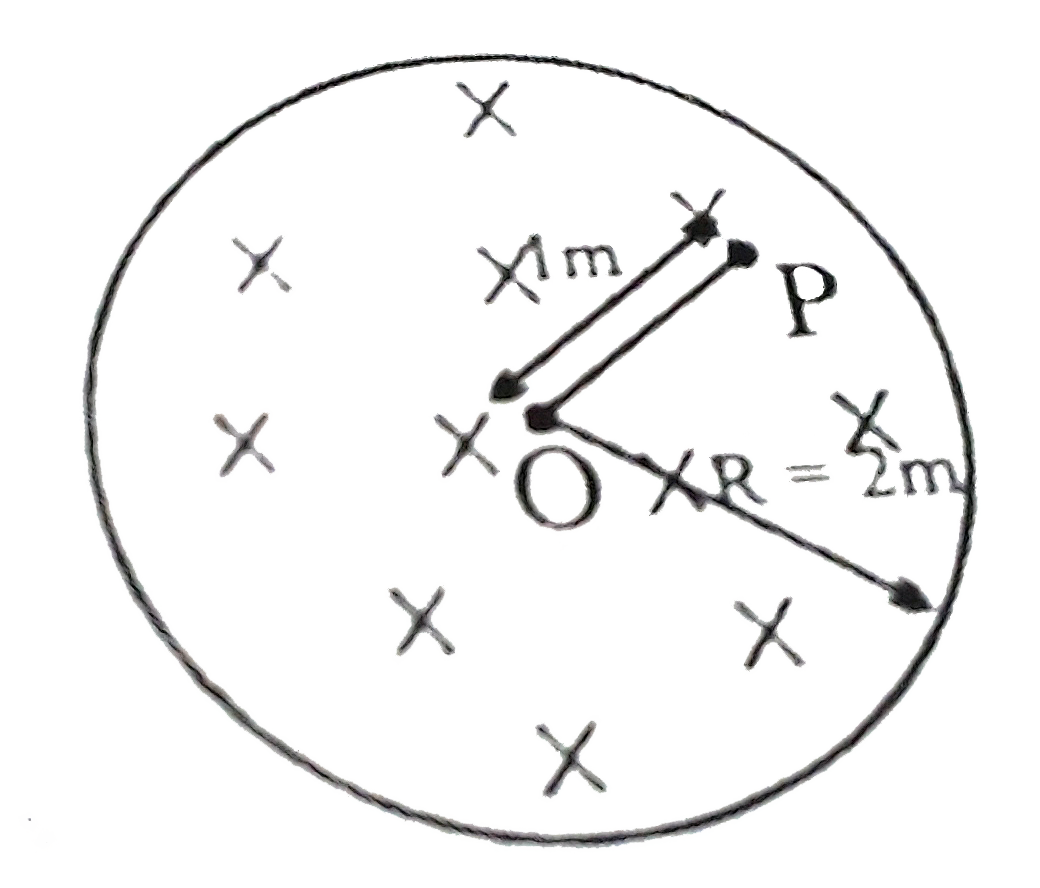
In the previous problem, the direction of circular electric lines at t=1s isView SolutionA uniform but time varying magnetic field exists in a cylindrical region as shown in the figure. The direction of magnetic field is into the plane of the paper and its magnitude is decreasing at a constant rate of 2×10−3T/s. A particle of charge 1μC is moved slowly along circle of radius 1m by an external force as shown in figure. The plane of the circle of radius 1m by an external force as shown in figure. The plane of he circle lies in the plane of the paper and it is concentric with the cylindrical region. The work done by the external force in moving this charge along the circle will be
 View Solution
View SolutionFigure shows a circular region of radius R in which uniform magnetic field B exists. The magnetic field is increasing at a rate dBdt. The induced electric field at a distance r from the centre for r<R is
 View Solution
View Solution

