A uniform magnetic field B exists perpendicular to the plane of the Figure in a circular region of radius b with its centre at O. A cir- cular conductor of radius a(<b) and centre at O is made by join- ing two semicircular wires ABC and ADC. The two segments have same cross section but different resistances R1 and R2 respectively. The magnetic field in increased with time and there is an induced current in the conductor.
(a) Find the ratio of electric fields inside the conductors ABC and ADC.
(b) Explain why the electric field in two conductors is different despite the fact that the magnetic field is symmetrical.

The correct Answer is:(a) E1E2=R1R2
Step by step video, text & image solution for A uniform magnetic field B exists perpendicular to the plane of the Figure in a circular region of radius b with its centre at O. A cir- cular conductor of radius a ( lt b) and centre at O is made by join- ing two semicircular wires ABC and ADC. The two segments have same cross section but different resistances R_(1) and R_(2) respectively. The magnetic field in increased with time and there is an induced current in the conductor. (a) Find the ratio of electric fields inside the conductors ABC and ADC. (b) Explain why the electric field in two conductors is different despite the fact that the magnetic field is symmetrical. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
There is a uniform magnetic field (B) perpendicular to the plane of the figure in a circular region of radius a centred at O. ABCD is a conducing loop in the plane of the figure with its arms BC and DA along two radial lines from O having an angle θ between them. AB is circular arc of radius OB = d centred at O. CD is also a circular arc of radius OC=b centred at O. The magnetic field is changed at a rate dBdt.
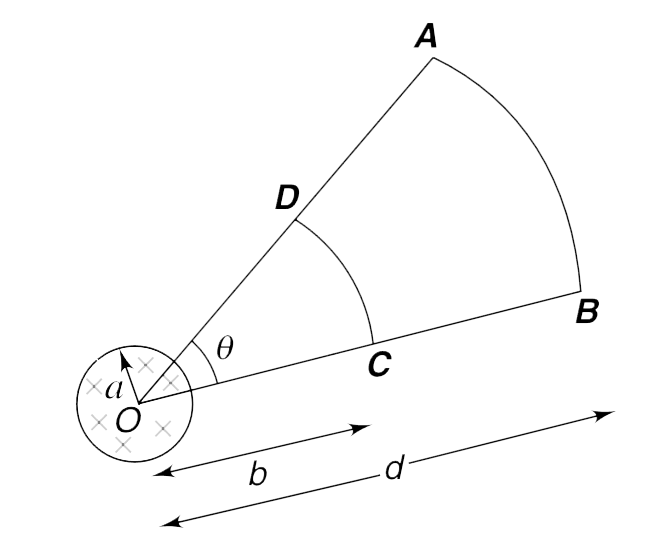
(a) The emf induced in the loop ABCD.
(b) Find emf induced in arc AB.
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
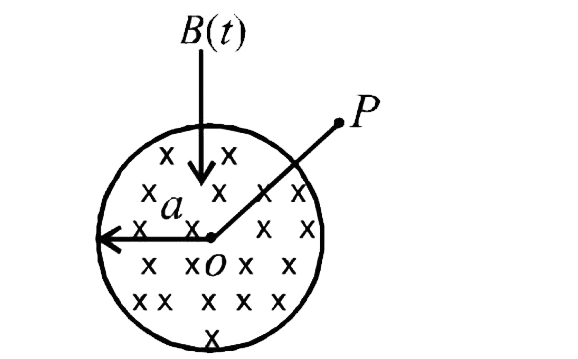
View Solution
Knowledge Check
Two coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is
A1:2B2:1C1:1D4:1A uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
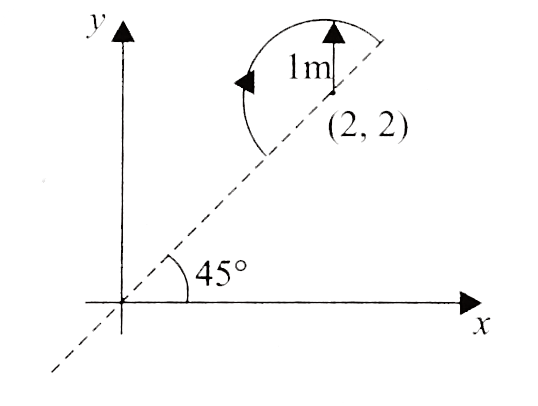 A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)
A√2(ˆi+ˆj+ˆk)B√2(ˆi−ˆj+ˆk)C√2(ˆi+ˆj−ˆk)D√2(−ˆi+ˆj+ˆk)A uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.
 Ais zeroBdecreases as 1rCincreases as rDdecreases as 1r2
Ais zeroBdecreases as 1rCincreases as rDdecreases as 1r2
A uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionMagnetic field at the centre of a circular coil of radius R due to curent i flowing through it is B. The magnetic field at a point along the axis at distance R from the centre is :
View SolutionA uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
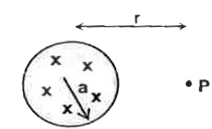
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionThe resistance of wire ABC is double of resistance of wire ADC. The magnetic field at O is

View Solution
