A uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
2Bqdm
Bqdm
Bq2dm
Bqd2m
The correct Answer is:D
To solve the problem, we need to analyze the motion of a charged particle in a magnetic field. Let's break down the solution step by step:
Step 1: Understand the Problem
We have a uniform magnetic field ¯B=B0^j and a particle with mass m and charge q projected towards the negative x-axis from the point (d,0,0). We need to find the maximum speed v such that the particle does not hit the y-z plane.
Step 2: Identify the Forces Acting on the Particle
When a charged particle moves in a magnetic field, it experiences a magnetic force given by the Lorentz force law:
¯F=q(¯vׯB)
Here, ¯v is the velocity of the particle and ¯B is the magnetic field.
Step 3: Determine the Direction of the Force
Since the particle is moving in the negative x-direction (let's denote this as −^i), and the magnetic field is in the positive y-direction (^j), we can calculate the force:
¯F=q(−^i×B0^j)=q(−B0^k)
This force acts in the negative z-direction, causing the particle to move in a circular path in the x-y plane.
Step 4: Calculate the Radius of the Circular Motion
The radius r of the circular motion of the particle can be determined using the formula:
r=mvqB0
Step 5: Condition for Not Hitting the y-z Plane
For the particle to not hit the y-z plane, the distance d from the origin must be greater than the diameter of the circular path. Therefore, we have the condition:
d>2r
Substituting the expression for r:
d>2(mvqB0)
Step 6: Rearranging the Inequality
Rearranging the inequality gives:
d>2mvqB0
From this, we can express v in terms of d:
v<qB0d2m
Step 7: Conclusion
The maximum value of v for which the particle does not hit the y-z plane is:
vmax=qB0d2m
Final Answer
Thus, the maximum speed v for which the particle does not hit the y-z plane is:
qB0d2m
We have a uniform magnetic field ¯B=B0^j and a particle with mass m and charge q projected towards the negative x-axis from the point (d,0,0). We need to find the maximum speed v such that the particle does not hit the y-z plane.
When a charged particle moves in a magnetic field, it experiences a magnetic force given by the Lorentz force law:
¯F=q(¯vׯB)
Here, ¯v is the velocity of the particle and ¯B is the magnetic field.
Since the particle is moving in the negative x-direction (let's denote this as −^i), and the magnetic field is in the positive y-direction (^j), we can calculate the force:
¯F=q(−^i×B0^j)=q(−B0^k)
This force acts in the negative z-direction, causing the particle to move in a circular path in the x-y plane.
The radius r of the circular motion of the particle can be determined using the formula:
r=mvqB0
For the particle to not hit the y-z plane, the distance d from the origin must be greater than the diameter of the circular path. Therefore, we have the condition:
d>2r
Substituting the expression for r:
d>2(mvqB0)
Rearranging the inequality gives:
d>2mvqB0
From this, we can express v in terms of d:
v<qB0d2m
The maximum value of v for which the particle does not hit the y-z plane is:
vmax=qB0d2m
Thus, the maximum speed v for which the particle does not hit the y-z plane is:
qB0d2m
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
Consider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.

View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on is
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
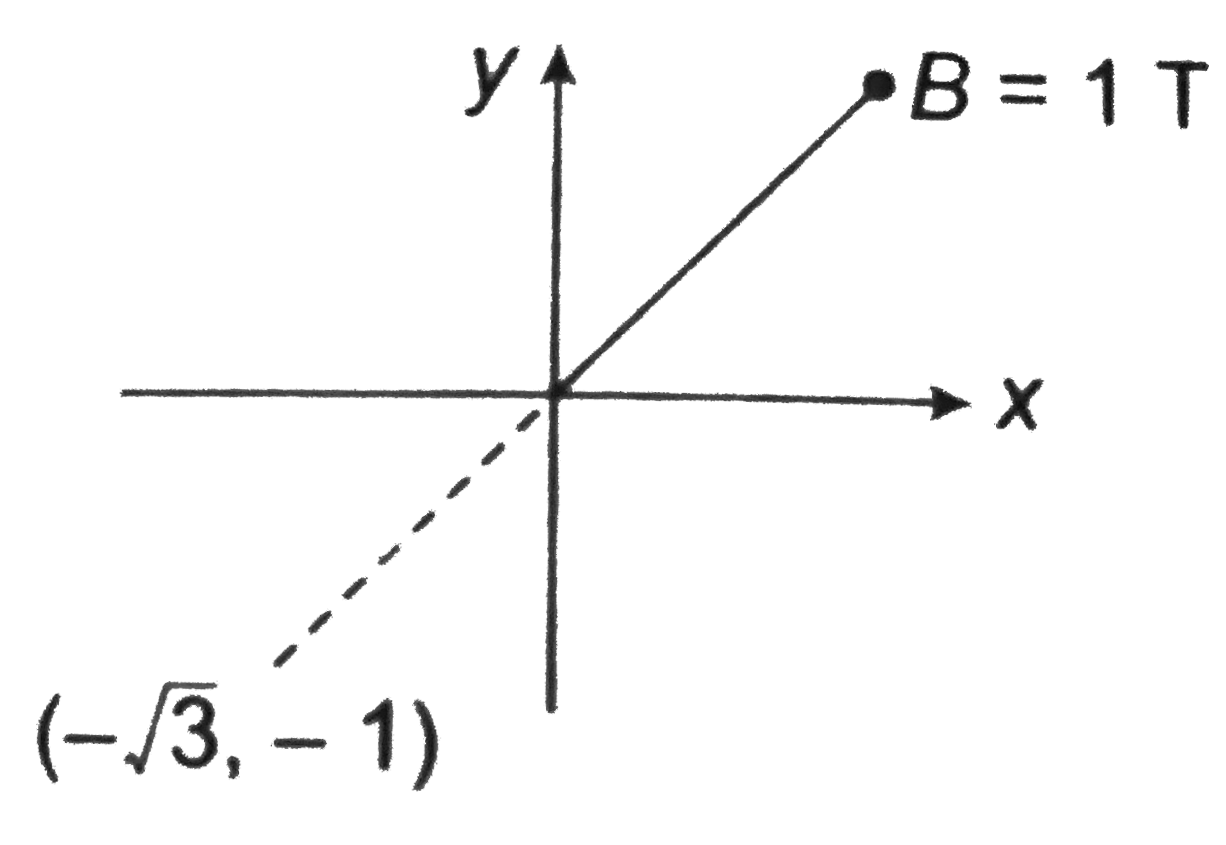
View SolutionA uniform magnetic field of magnitude 1T exists in region y≥0 along ˆk direction as shown. A particle of charge 1C is projected from point (−√3,−1) towards origin with speeds 1m/sec. If mass of particle moves are:
View SolutionTwo particle, each having a mass m are placed at a separation d in a uniform magnetic field B as shown in figure.They have opposite charges of equal magnitude q.At time t=0, the particles are projected towards each other, each with a speed v.
What would be the maximum separation between the particles if v=vm4?

View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point( 2a, b/2, 0) its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
View SolutionTwo particle, each having a mass m are placed at a separation d in a uniform magnetic field B as shown in figure.They have opposite charges of equal magnitude q.At time t=0, the particles are projected towards each other, each with a speed v.
What would be the minimum separation between the particles if v=vm4?

View Solution
