A uniform metre stick of mass 200 g is suspended from the ceiling through two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm fomd the left end. Find the tensions in the two strings.
The correct Answer is:A, B, D
To solve the problem of finding the tensions in the two strings supporting the uniform metre stick with a small object placed on it, we can follow these steps:
Step 1: Identify the forces acting on the system
The forces acting on the system include:
- The weight of the metre stick (W1)
- The weight of the small object (W2)
- The tensions in the two strings (T1 and T2)
Step 2: Calculate the weights
1. The mass of the metre stick (m1) is 200 g, which is 0.2 kg.
- Weight of the metre stick (W1) = m1 * g = 0.2 kg * 9.81 m/s² = 1.962 N
2. The mass of the small object (m2) is 20 g, which is 0.02 kg.
- Weight of the small object (W2) = m2 * g = 0.02 kg * 9.81 m/s² = 0.1962 N
Step 3: Set up the equations of equilibrium
Since the system is in equilibrium, the sum of the vertical forces must equal zero, and the sum of the moments about any point must also equal zero.
1. Vertical Forces:
T1+T2=W1+W2
T1+T2=1.962N+0.1962N=2.1582N
2. Moments about the left end of the stick:
Taking moments about the left end (point A), we have:
- The moment due to T2 (acting at 1 m from the left end) is counterclockwise.
- The moment due to W1 (acting at the center of the stick, 0.5 m from the left end) is clockwise.
- The moment due to W2 (acting at 0.7 m from the left end) is clockwise.
The moment equation is:
T2⋅1=W1⋅0.5+W2⋅0.7
Substituting the values:
T2⋅1=(1.962N⋅0.5)+(0.1962N⋅0.7)
T2=0.981N+0.13734N=1.11834N
Step 4: Solve for T1
Using the vertical forces equation:
T1+T2=2.1582N
Substituting T2:
T1+1.11834N=2.1582N
T1=2.1582N−1.11834N=1.03986N
Final Results
- Tension in the first string (T1) = 1.03986 N
- Tension in the second string (T2) = 1.11834 N
The forces acting on the system include:
- The weight of the metre stick (W1)
- The weight of the small object (W2)
- The tensions in the two strings (T1 and T2)
1. The mass of the metre stick (m1) is 200 g, which is 0.2 kg.
- Weight of the metre stick (W1) = m1 * g = 0.2 kg * 9.81 m/s² = 1.962 N
2. The mass of the small object (m2) is 20 g, which is 0.02 kg.
- Weight of the small object (W2) = m2 * g = 0.02 kg * 9.81 m/s² = 0.1962 N
Since the system is in equilibrium, the sum of the vertical forces must equal zero, and the sum of the moments about any point must also equal zero.
T1+T2=W1+W2
T1+T2=1.962N+0.1962N=2.1582N
Taking moments about the left end (point A), we have:
- The moment due to T2 (acting at 1 m from the left end) is counterclockwise.
- The moment due to W1 (acting at the center of the stick, 0.5 m from the left end) is clockwise.
- The moment due to W2 (acting at 0.7 m from the left end) is clockwise.
T2⋅1=W1⋅0.5+W2⋅0.7
Substituting the values:
T2⋅1=(1.962N⋅0.5)+(0.1962N⋅0.7)
T2=0.981N+0.13734N=1.11834N
Using the vertical forces equation:
T1+T2=2.1582N
Substituting T2:
T1+1.11834N=2.1582N
T1=2.1582N−1.11834N=1.03986N
- Tension in the first string (T1) = 1.03986 N
- Tension in the second string (T2) = 1.11834 N
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A uniform rod of mass m and length L is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass 2m is placed at distance L/4 from the left end. Find the tensions in the two strings.
View SolutionA 1 m rod of mass 100 kg is hanging from two in extensible support strings at its ends of equal lengths. If an another mass of 20 kg is placed on rod at a distance 30 cm from the left end, find the tension in the two support strings, if rod remains horizontal. Take g=10m/s2
[560 N, 640 N]
View Solution
Knowledge Check
A uniform horizontal metre scale of mass m is suspended by two vertical strings attached to its two ends. A body of mass 2m is placed on the 75 cm mark. The tensions in the two strings are in the ratio is
A1:2B1:3C2:3D3:4A uniform horizontal meter scale of mass m is suspended by two vertical strings attached to its two ends. A block of mass 3m is placed on the 60cm mark. The tensions in the two strings are in the ratio
A17:19B19:21C17:23D19:23A uniform horizontal meter scale of mass m is susopended by two certical string attached to its two ends. A body of mass 2m is place on the 75−cm mark. The tensions in the two strings are in the ratio
A1:2B1:3C2:3D3:4
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
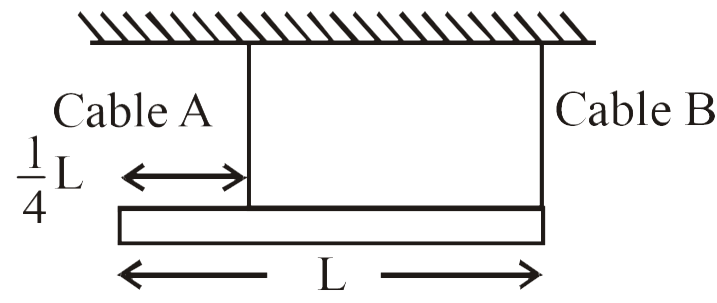
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
View SolutionA horizontal rod of length 5m weight 4 kg is suspended at the ends by two strings. The weights 8 kg, 12 kg, 16 kg and 20 kg are placed on the rod at distance 1 m, 2 m, 3 m and 4 m from one end of the rod. Then the tensions in the string are
View Solution
