A uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
V02
V04
3V04
0
The correct Answer is:B
Here u=V0,ω0=V02R
At pure rolling 
and VR=−V02R=(fmR)t
(in pure rolling V=Rω)
(α=τI=fRmR2=fmR)
V0−V=V+V02
2V=V02⇒V=V04
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA uniform ring of mass m and radius R is performing pure rolling motion on a horizontal surface. The velocity of centre of the ring is V0. If at the given instant the kinetic energy of the semi circular are AOB is lambda mv0_(2), then find the value of 11λ(takeπ=227)
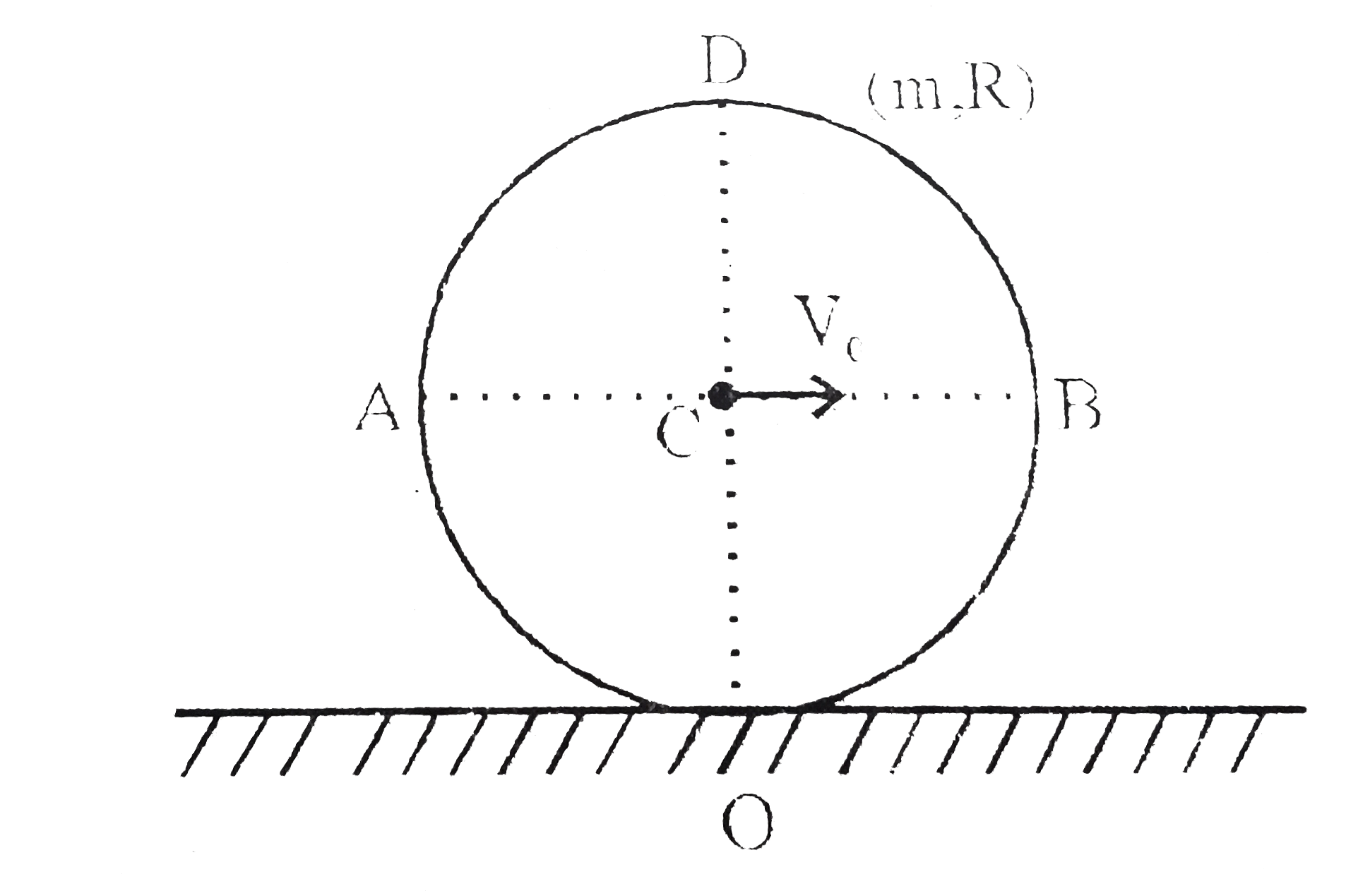 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
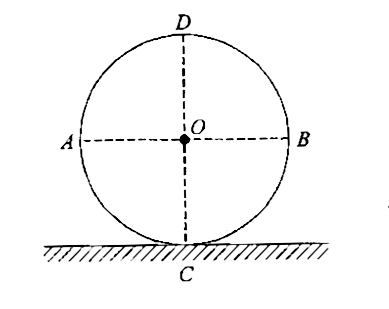
A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20 - Question 2 - Select One
A hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
Arω02Brω0Crω04Drω03 - Question 3 - Select One
A hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
Arω04Brω03Crω02Drω0
A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA uniform disc of mass m and radius R is given a velocity v0 and angular velocity ω0 as shown and released of a fixed horizontal surface. Only the x length of the surface is rough. Find the minimum value of x (in metres) so that disc starts pure rolling. Use ω20R272μg=1m
 View Solution
View SolutionA cylinder is rotating with angular velocity ω0 and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
View SolutionA heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
View SolutionA sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre V02r. The translational velocity when the sphere starts pure rolling motion is
View Solution

