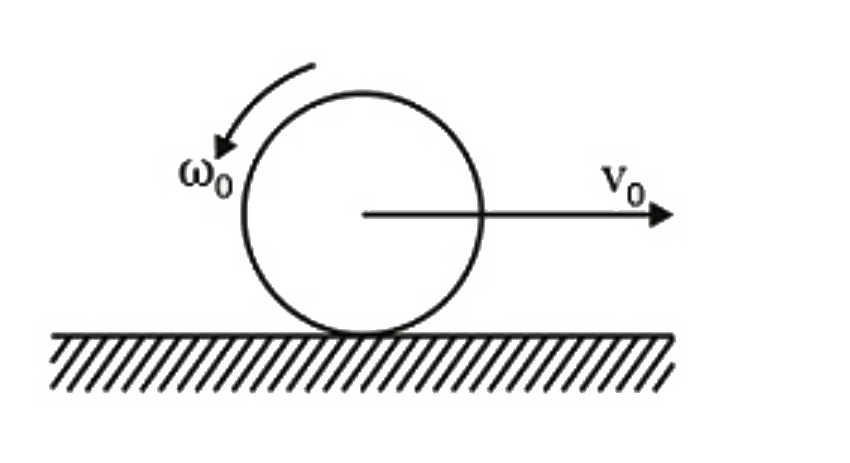
A uniform disc of mass $m$ and radius $R$ is given a velocity $v_{0}$ and angular velocity $ω_{0}$ as shown and released of a fixed horizontal surface. Only the $x$ length of the surface is rough. Find the minimum value of $x$ (in metres) so that disc starts pure rolling. Use $\frac{ω_{0}^{2} R^{2}}{72 μ g} = 1 m$

Text Solution

Verified by Experts

The correct Answer is:7

$\frac{m ω_{0} R^{2}}{2} + \frac{m R^{2}}{2} ω_{0} = m ω_{0} R^{2} + \frac{m R^{2}}{2} ω$
$\Rightarrow ω_{0} = \frac{3}{2} ω \Rightarrow ω = \frac{2 ω_{0}}{3}$
$\Rightarrow v = ω R = \frac{2}{3} ω_{0} R = \frac{4 v_{0}}{3}$
$= \frac{16 v_{0}^{2}}{9} = v_{0}^{2} + 2 μ g x$
$2 μ g x = \frac{7 v_{0}^{2}}{9} \Rightarrow x = \frac{7 v_{0}^{2}}{18 μ g} = \frac{7 ω_{0}^{2} R^{2}}{72 μ g} = 7 m$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A uniform circular disc of radius $r$ is placed on a rough horizontal surface and given a linear velocity $v_{0}$ and angular velocity $ω_{0}$ as shown. The disc comes to rest after moving some distance to the right. It follows that

A $3 v_{0} = 2 ω_{0} r$
B $2 v_{0} = ω_{0} r$
C $v_{0} = ω_{0} r$
D $2 v_{0} = 3 ω_{0} r$
Question 2 - Select One
A disc is given an angular velocity $ω_{0}$ and a linear velocity $v_{0}$ as shown in the figure. It is released on a rough horizontal surface of friction coefficient $μ .$ Mark the correct statement $(ω_{0} = 3 v_{0} / R)$
AThe frictional force will be $μ$ mg during the entire motion.
BAfter some time the disc will start rolling without sliding along positive x-axis.
CAfter some time the disc will start rolling without sliding along negative x-axis.
DThe mechnical energy of the disc will remain conserved.
Question 3 - Select One or More
A disc is given an initial angular velocity $ω_{0}$ and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

Athe time until rolling begins
Bthe displacement of the disc until rolling begins
Cthe velocity when rolling begins
Dthe work done by the force of friction

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile