A uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?

a. Using work energy theorem WF+Wgr=△K
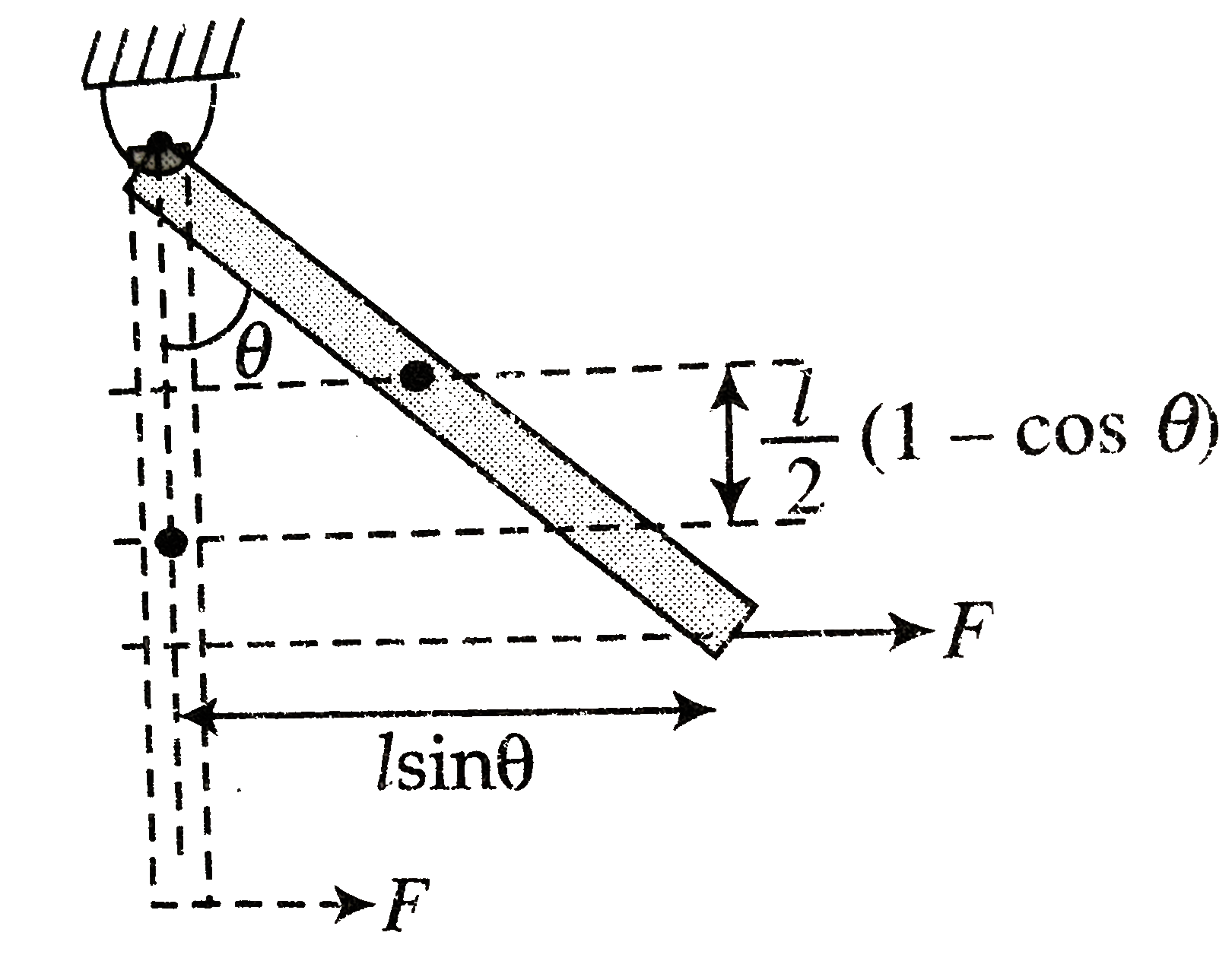
Flsinθ−mgl2(1−cosθ)−12(ml23)ω2
ω=(6Fmlsinθ−3g1−cosθ)
b. At maximum angular displacement put ω=0 in eqn
0=√6Emlsinθ−3g1−cosθ
⇒6Emlsinθ=3gl(1−cosθ)
⇒2Em(2sinθ2.cosθ2)=g(2sin2θ2)
⇒tanθ2=2Fmg⇒θ=2tan−1(2Fmg)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 View Solution
View SolutionA rod of length l is pivoted smoothly at O is resting on a block of height h. If the block moves with a constant velocity V, pick the correct alternatives about angular velocity of rod :
 View Solution
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?
 View Solution
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
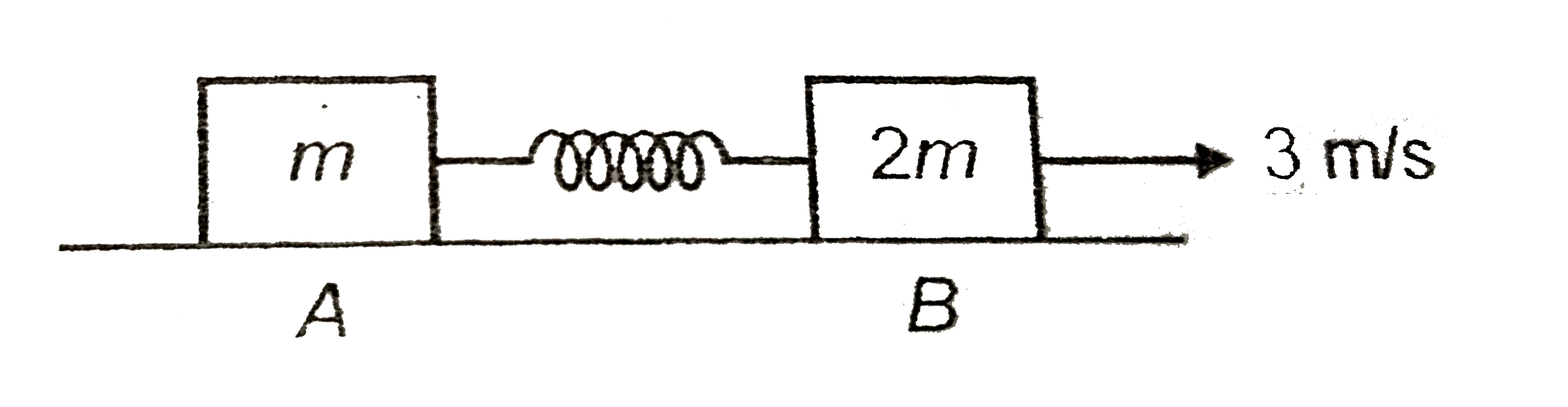 View Solution
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.
 View Solution
View SolutionA thin rigid insulated rod of mass m and length l carrying a charge Q unformly distrivuted along its length is smoothly pivoted at P. It is palced in between the charged large conducting plates. Disregard gravity.
(a) Find the initial accelaeration of the rod.
(b) Find the angular speed of the rod as the function of angel θ of rotation ω=f(θ), if the rod is allowed to rotate freely .
 View Solution
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate a. the angular momentum of the rod about the axis of rotation b. the speed of the centre of the rod and c. its kinetic energy.
View Solution
