A uniform rod of mass and length rotates in a horizontal plane with an angular velocity about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
To find the tension in a uniform rod of mass m and length l rotating in a horizontal plane with an angular velocity ω about a vertical axis passing through one end, we can follow these steps:
1. Understanding the System:
- We have a uniform rod of length l and mass m rotating about a vertical axis at one end with angular velocity ω. We need to find the tension in the rod at a distance x from the axis of rotation.
2. Identifying the Element of the Rod:
- Consider a small segment of the rod at a distance x from the axis. The length of the segment from x to the end of the rod is l−x.
3. Finding the Mass of the Segment:
- The linear mass density (λ) of the rod is given by:
\(
\lambda = \frac{m}{l}
\)
- The mass of the segment (m') from x to l is:
\(
m' = \lambda \cdot (l - x) = \frac{m}{l} \cdot (l - x)
\)
4. Centripetal Acceleration:
- The segment at distance x from the axis has to provide centripetal force for the mass of the segment. The radius of circular motion for the center of mass of this segment is:
\(
r = x + \frac{l - x}{2} = x + \frac{l}{2} - \frac{x}{2} = \frac{l}{2} + \frac{x}{2}
\)
- The centripetal acceleration (a_c) is given by:
\(
a_c = \omega^2 r = \omega^2 \left(\frac{l}{2} + \frac{x}{2}\right)
\)
5. Centripetal Force:
- The required centripetal force (F_c) for the segment is:
\(
F_c = m' a_c = \left(\frac{m}{l} (l - x)\right) \cdot \left(\omega^2 \left(\frac{l}{2} + \frac{x}{2}\right)\right)
\)
6. Tension in the Rod:
- The tension (T) in the rod at distance x must provide the necessary centripetal force for the mass of the segment:
\(
T = F_c = \frac{m}{l} (l - x) \cdot \omega^2 \left(\frac{l}{2} + \frac{x}{2}\right)
\)
7. Final Expression for Tension:
- Simplifying the expression for tension:
\(
T = \frac{m \omega^2}{l} (l - x) \left(\frac{l}{2} + \frac{x}{2}\right)
\)
- This can be further simplified to:
\(
T = \frac{m \omega^2}{2l} (l - x)(l + x) = \frac{m \omega^2}{2l} (l^2 - x^2)
\)
Final Result:
The tension in the rod at a distance x from the axis is:
\(
T = \frac{m \omega^2}{2l} (l^2 - x^2)
\)
- We have a uniform rod of length l and mass m rotating about a vertical axis at one end with angular velocity ω. We need to find the tension in the rod at a distance x from the axis of rotation.
- Consider a small segment of the rod at a distance x from the axis. The length of the segment from x to the end of the rod is l−x.
- The linear mass density (λ) of the rod is given by:
\(
\lambda = \frac{m}{l}
\)
- The mass of the segment (m') from x to l is:
\(
m' = \lambda \cdot (l - x) = \frac{m}{l} \cdot (l - x)
\)
- The segment at distance x from the axis has to provide centripetal force for the mass of the segment. The radius of circular motion for the center of mass of this segment is:
\(
r = x + \frac{l - x}{2} = x + \frac{l}{2} - \frac{x}{2} = \frac{l}{2} + \frac{x}{2}
\)
- The centripetal acceleration (a_c) is given by:
\(
a_c = \omega^2 r = \omega^2 \left(\frac{l}{2} + \frac{x}{2}\right)
\)
- The required centripetal force (F_c) for the segment is:
\(
F_c = m' a_c = \left(\frac{m}{l} (l - x)\right) \cdot \left(\omega^2 \left(\frac{l}{2} + \frac{x}{2}\right)\right)
\)
- The tension (T) in the rod at distance x must provide the necessary centripetal force for the mass of the segment:
\(
T = F_c = \frac{m}{l} (l - x) \cdot \omega^2 \left(\frac{l}{2} + \frac{x}{2}\right)
\)
- Simplifying the expression for tension:
\(
T = \frac{m \omega^2}{l} (l - x) \left(\frac{l}{2} + \frac{x}{2}\right)
\)
- This can be further simplified to:
\(
T = \frac{m \omega^2}{2l} (l - x)(l + x) = \frac{m \omega^2}{2l} (l^2 - x^2)
\)
The tension in the rod at a distance x from the axis is:
\(
T = \frac{m \omega^2}{2l} (l^2 - x^2)
\)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution
Knowledge Check
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)A uniform rod of length l is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from the axis, then which of the following graphs depicts it most closely ?
A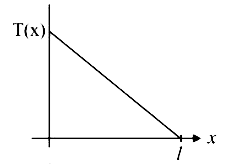 B
B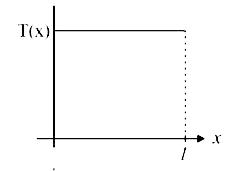 C
C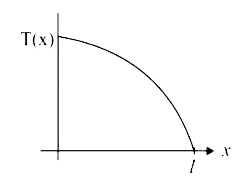 D
D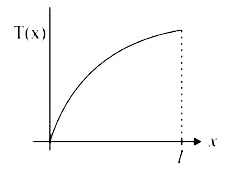
A thin uniform copper rod length l and mass m rotates unifomly with an angular velocity ω about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is σmax, cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions

The maximum angular velocity with which the rod can rotate so that is won't break, isA√2σmaxAmlB√2σmaxA3mlC√σmaxA2mlD√3σmaxAml
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
View SolutionA rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed ω about a vertical axis passing through A. If coefficient of linear expansion of material of rod is α, find the percentage change in its angular velocity if temperature of system is incresed by ΔT
View SolutionA rigid rod of mass m and lengths l, is being rotated in horizontal plane about a vertical axis, passing through one end A. If TA,TBandTC are the tensions in rod at point A, mid point B and point C of rod repsectively, then

View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View Solution
