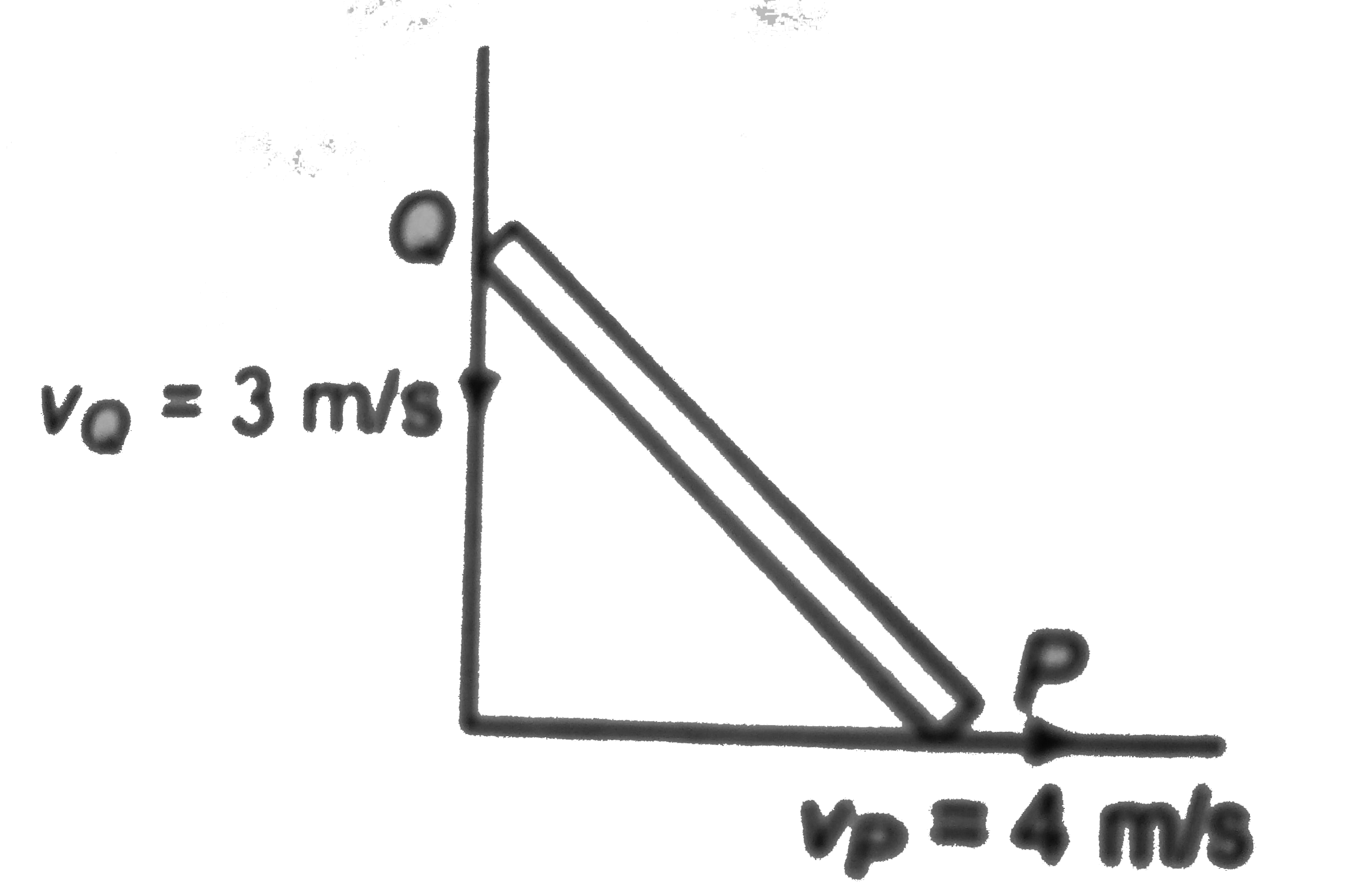
A uniform rod of mass m=2kg and length l=0.5m is sliding along two mutually perpendicular smooth walls with the two ends P and Q having velocities UP=4m/s and vQ=3m/s as shown then
The angular velocity of rod, ω=10rad/s counter clockwise
The angular veloicty of rod ω=5.0rad/s counter clockwie
The velocity of centre of mass of rod vcm=2.5m/s
The total kinetic energy of rod, K=253joule

x2+y2=l2=(0.25)m2
yω=4 ..(i)
xω=3 ..(ii)
Squaring and adding we get
(x2+y2)ω2=25
or (0.25)ω2=25
∴ω=10rad/s
OC=l2=0.25m
Ktotal=12mv2cm+12Icmω2
=12×2×(0.25)2+12(2×0.2512)(10)2
=253J
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angulr velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View SolutionA uniform rod AB of mass m=2kg and length l=1.0m is placed on a sharp support P such that a=0.4m and b=0.6m. A. spring of force constant k=600N/m is attached to end B as shown in Fig. To keep the rod horizontal, its end A is tied with a thread such that the spring is B elongated by 1CM. Calculate reaction of support P when the thread is burnt.
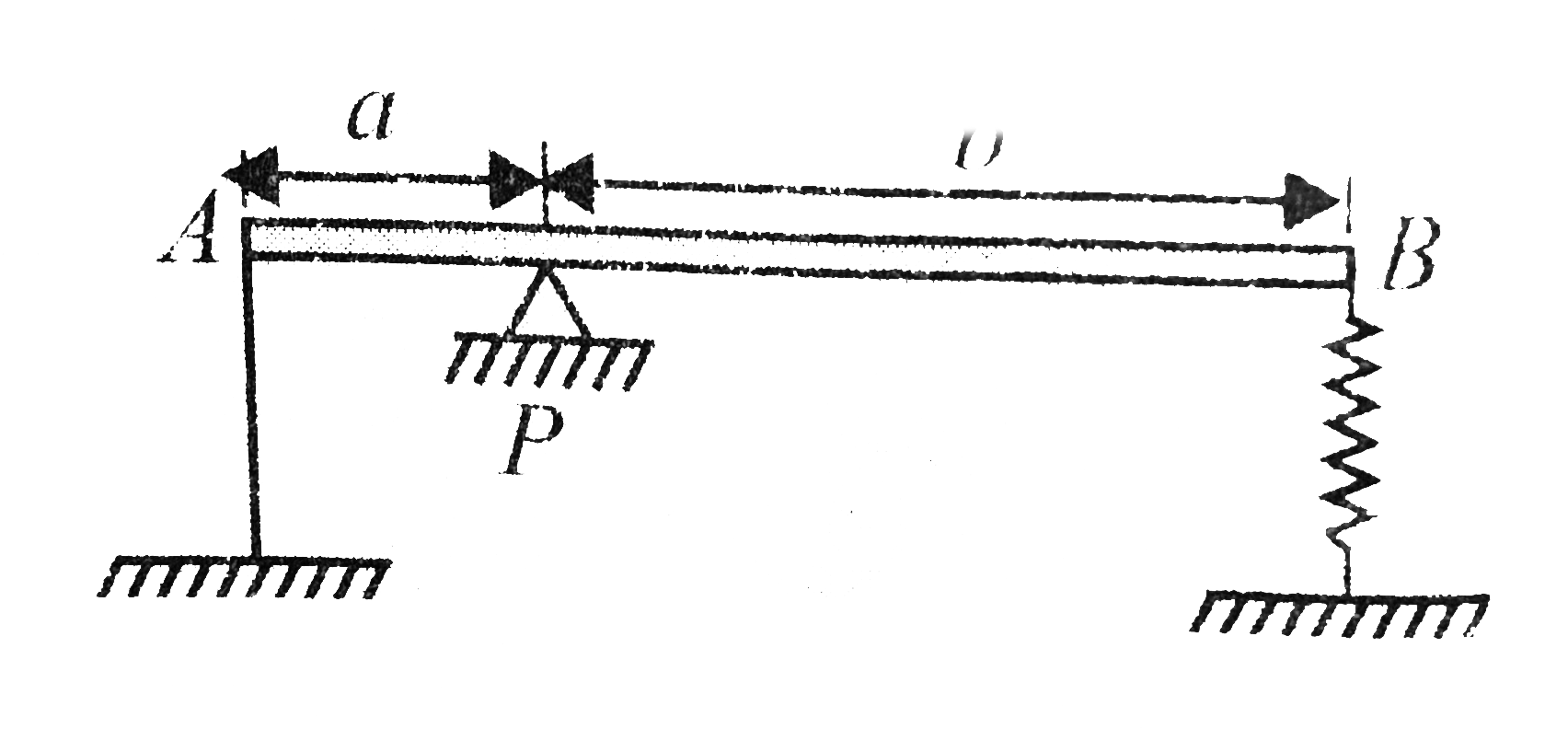
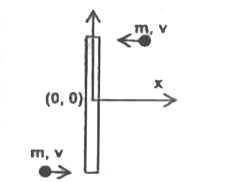
View SolutionA rigid uniform rod of mass M and length L is placed along the Y-axis on a smooth horizontal surface with its centre at the origin. Two particles , each of mas m(=M/12) hits simultaneously , at the two ends with equal speed v as shown in the figure. The collision is completely inelastic.
(i) Find the angular velocity of the system after the collision.
(ii) Two particles of mass 2m and m are placed respectively at ( L/2,0) and (−L/2,0). Calculate the time when the rod hits these particles.
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
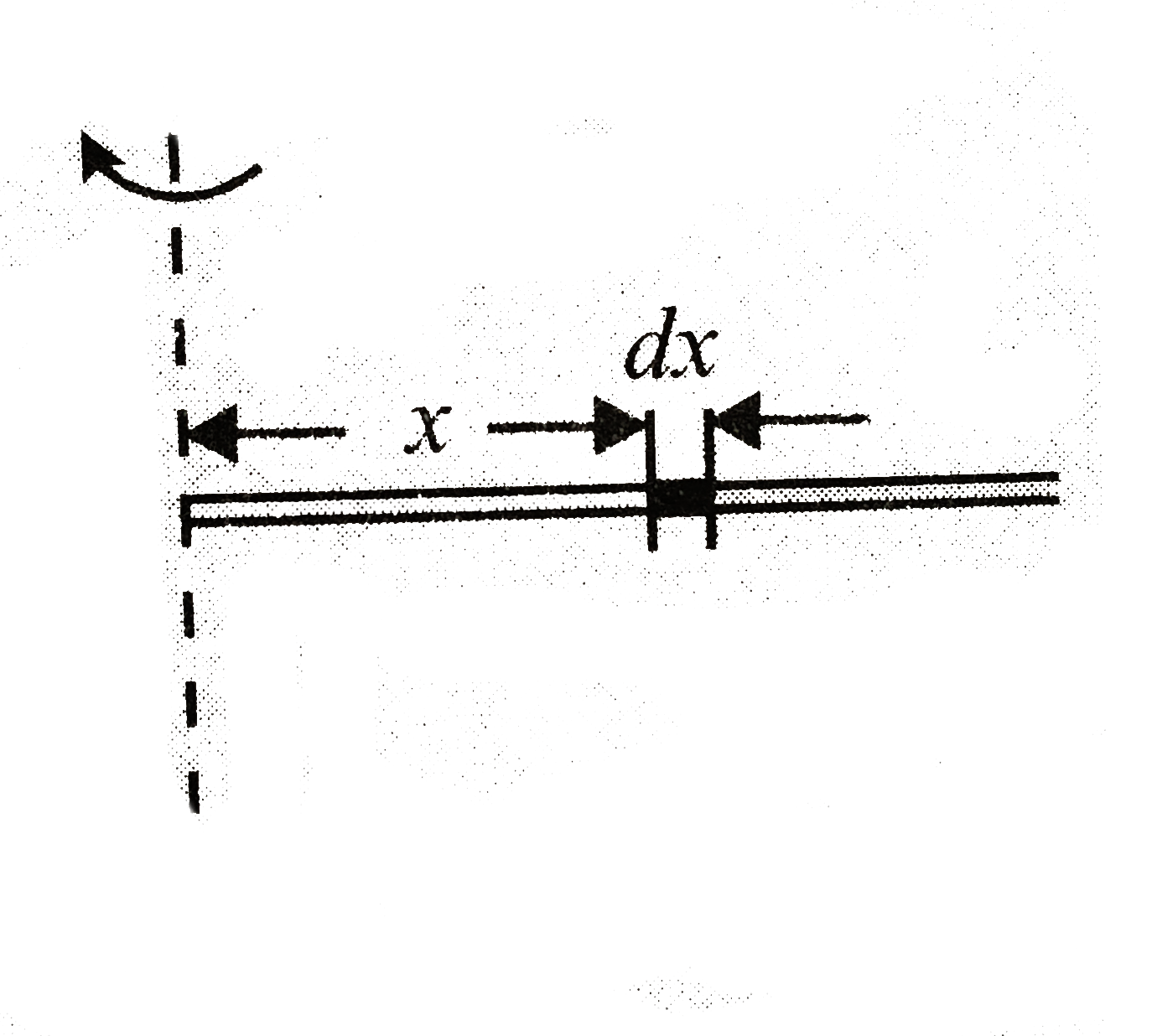
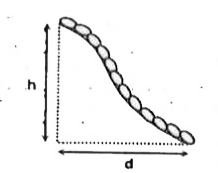
View SolutionA uniform chain of mass per unit length λ is sliding down the hill with constant speed u. Dimension of the hill are h and d as shown. Find the momentum of the chain at the instant shown. (given λ=1kg/m,d=3m,h=4m,andu=1m/s)
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
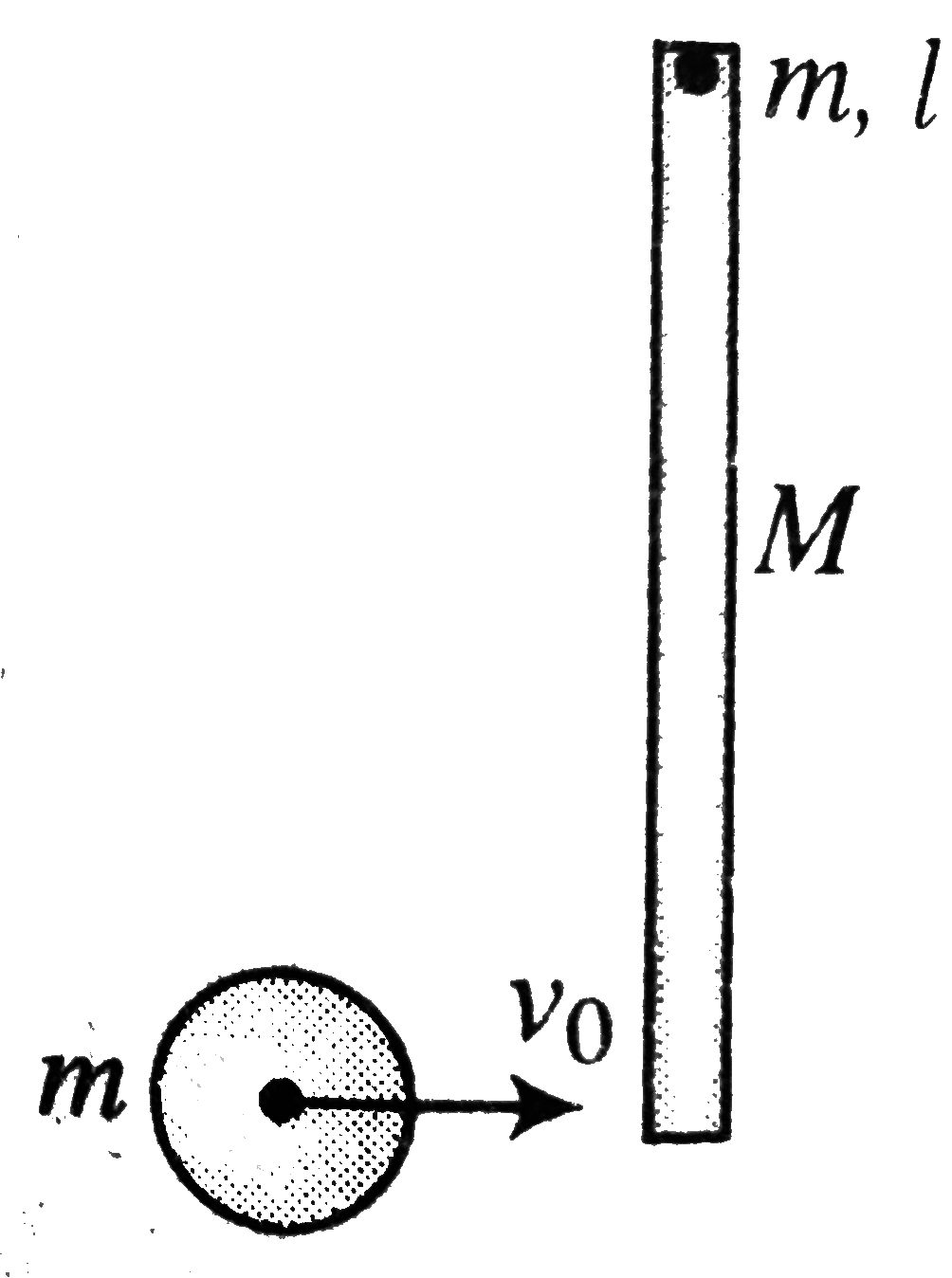
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod of mass M and length L falls when it is made to stand on a smooth horizontal floor. The trajectories of the points P,Q and R as shown in the figure given below is best represented by :
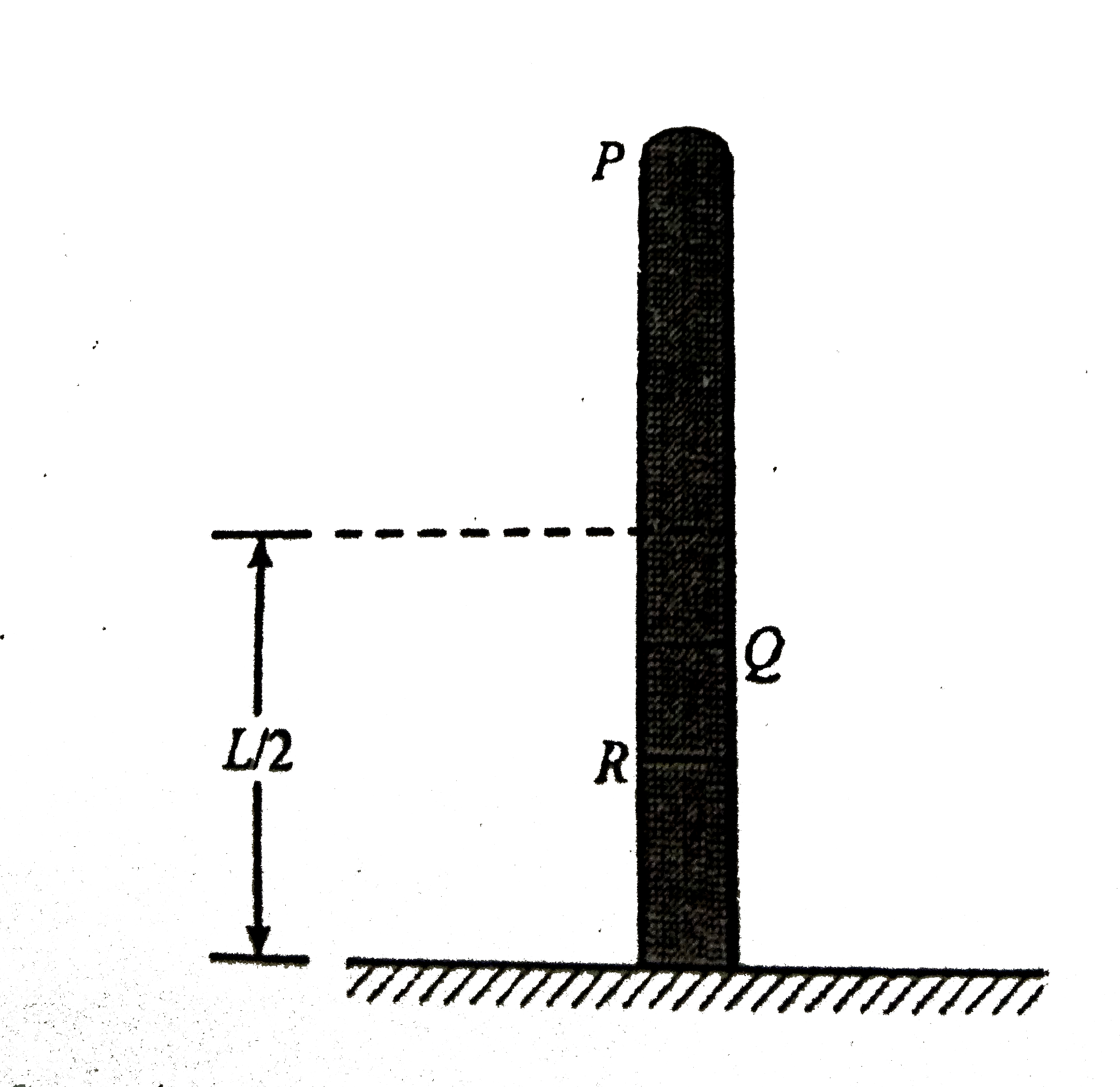
View SolutionA horizontal rod of mass M and length L is tied to two verticle string symmetrically as shown in the figure. One of the strings at end Q is cut at t=0 and the rod starts rotating about the other and P then

View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View Solution
