A uniform rope of length 12m and mass 6kg hangs vertically from a rigid support. A block of mass 2kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
 As the rope is heavy, its tension will be different at different points. The tension at thefree end will be 2 g and thatat the upper end it will be 8 g.
As the rope is heavy, its tension will be different at different points. The tension at thefree end will be 2 g and thatat the upper end it will be 8 g.
we have v=nλ
√Tμ=nλ
√Tλ=n√μ
The frequency of thewave pulse will be the same every where on the rope as it depends onlyonthe frequency ofthesource. The mass perunitlength isalso the same throughout the rope as it is uniform. Thus, we have
As√Tλ is constant, we have
√2g0.06m=√8gλ1
Solving we get λ1 = 0.12 m
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.1
12 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.2
11 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
A uniform rope of length 12m and mass 6kg hangs vertically from a rigid support . A block of mass 2kg is attached to the free end of the rope . A transverse pulse of wavelengths 0.06m is produced at the lower end of the rope . What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View Solution
Knowledge Check
A uniform rope of length 10 m and mass 3 kg hangs vertically from a rigid support. A block of mass 1 kg is attached to the free end of the rople. A transverse pulse of wavelength 0.05 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is
A0.10 mB0.12 mC0.16 mD0.18 mA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
A√m1+m2m1B√m1m2C√m1+m2m2D√m2m1A uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
A√m1m2B√m1+m2m2C√m2m1D√m1+m2m1
A uniform rope of length 20m and mass 8kg hangs vertically froma rigid support. A block of mass 2kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top os the rope?
View SolutionA uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 10 m and mass 15 kg hangs vertically from a rigid support. A block of mass 5 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.08 m is produced at the lower end of the 3 rope. The wavelength of the pulse when it reaches the top of the rope will be-
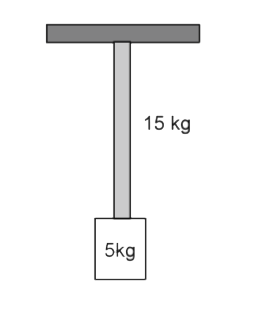
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
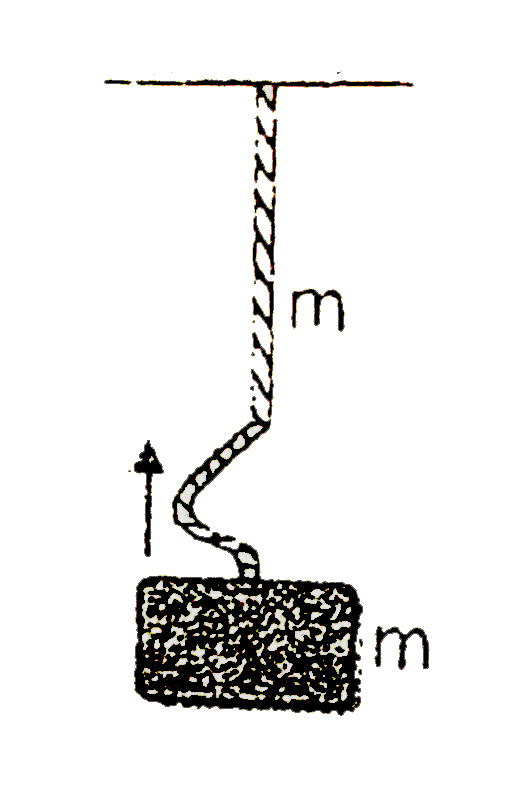
View SolutionA uniform rope of length L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View Solution
