A uniform rope of length L , resting on frictionless horizontal table is pulled at one end by a force F . What is the tension in the rope at a distance x from the end where the force is applied ?
[ Hint : Consider the motion of the entire rope and the motion of x length of rope using P = ma formula and third law of motion ]
The correct Answer is:T=F(1−x/L)
To solve the problem of finding the tension in a uniform rope of length L being pulled by a force F at one end, we can follow these steps:
Step 1: Analyze the entire rope
When the force F is applied to the end of the rope, the entire rope will accelerate. We can use Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F=ma).
Let the mass per unit length of the rope be λ. Therefore, the total mass m of the rope is given by:
m=λL
The acceleration a of the entire rope can be expressed as:
F=ma⟹a=Fm=FλL
Step 2: Consider a segment of the rope
Now, let’s consider a segment of the rope that is x long from the end where the force is applied. The mass of this segment mx is:
mx=λx
Step 3: Apply Newton's second law to the segment
The segment of the rope will also experience the same acceleration a as the entire rope. Therefore, applying Newton's second law to this segment, we have:
T=mxa
where T is the tension in the rope at a distance x from the end where the force is applied.
Substituting mx and a into the equation gives:
T=λx⋅FλL
Step 4: Simplify the expression for tension
Now, we can simplify the expression for tension T:
T=λxFλL=xFL
Final Result
Thus, the tension in the rope at a distance x from the end where the force is applied is given by:
T=xFL
When the force F is applied to the end of the rope, the entire rope will accelerate. We can use Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F=ma).
m=λL
The acceleration a of the entire rope can be expressed as:
F=ma⟹a=Fm=FλL
Now, let’s consider a segment of the rope that is x long from the end where the force is applied. The mass of this segment mx is:
mx=λx
The segment of the rope will also experience the same acceleration a as the entire rope. Therefore, applying Newton's second law to this segment, we have:
T=mxa
where T is the tension in the rope at a distance x from the end where the force is applied.
T=λx⋅FλL
Now, we can simplify the expression for tension T:
T=λxFλL=xFL
Thus, the tension in the rope at a distance x from the end where the force is applied is given by:
T=xFL
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)34videos
LAWS OF MOTION, FREE BODY DIAGRAM
- BOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)34videos
LAWS OF MOTION, FREE BODY DIAGRAM
- BOOK - NN GHOSHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions24videos
KINETIC THEORY OF GASES
- BOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises33videos
MOMENT, TORQUE, EQUILIBRIUM OF BODIES
Similar Questions
A uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the ropww at a distance l from the end where it is applied?
View Solution
Knowledge Check
- Question 1 - Select One
A rope of length 4 m having mass 1.5 kg/m lying on a horizontal frictionless surface is pulled at one end by a force of 12N. What is the tension in the rope at a point 1.6 m from the other end?
A5NB4.8NC7.2ND6N - Question 2 - Select One
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBF should be equal to the weight of A and BCF(L-x)/LDF(L-x)M - Question 3 - Select One
A rope of length 5 m is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 1 m from this end
A1 NB3 NC4 ND5 N
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
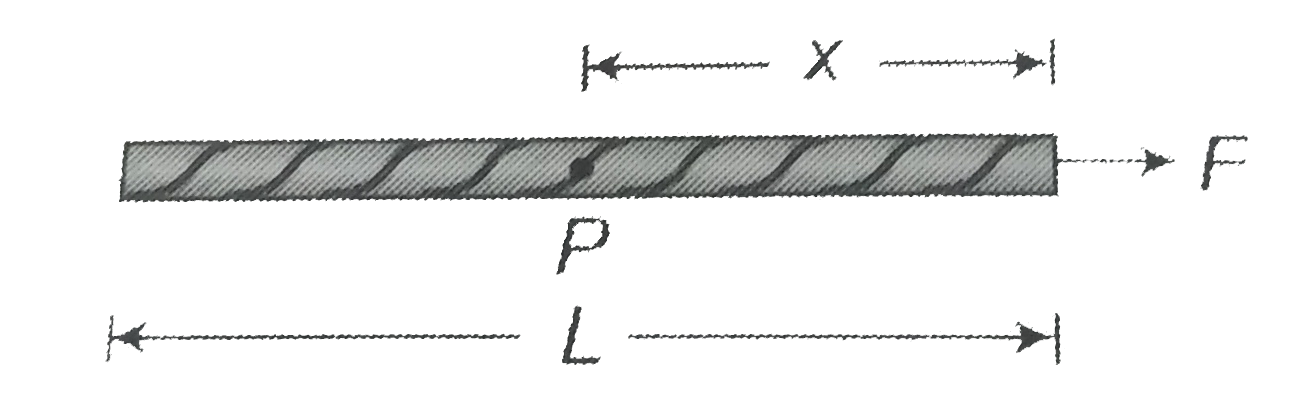 View Solution
View SolutionA horizontal force is applied on a uniform rod of length L kept on a frictionless surface. Find the tension in rod at a distance 'x' from the end where force is applied
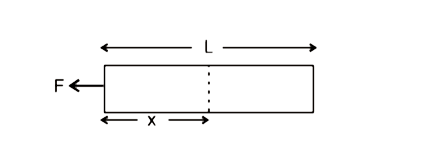 View Solution
View SolutionA uniform rope of mass M and length L, on which a force F is applied at one end, then find stress in the ropw at a distance x form the end where force is applied?
View SolutionA rope of length 20 cm is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 5m from this end.
View SolutionA uniform thick string of length 5 m is resting on a horizontal frictionless surface. It is pulled by a horizontal force of 5 N from one end. The tension in the string at 1m from the force applied is :
View Solution

