A uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a. Find the gravitational field at a distance a). 3/2 a from the centre , b). 5/2 as from the centre.
The correct Answer is:A, B, C, D
At distance 3a2 which lies between solid sphere and shell field is only due to solid sphere.
E=GM(3a/2)2=4GM9a2 (towards centre)
(b) At distance 5a2 which lies outside the shell. So, field strength is due to both
∴E=G(M+M)(5a/2)2=8GM25a2(towards centre)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Single Correct
27 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherica shel of equla mass and radius 2a.Find the gravitational field at a distance a. 3/2 a from the centre , b. 5/2 as from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View Solution
Knowledge Check
A uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
AThe gravitational field at a distance of 1.5r from the centre is 29Gmr2BThe gravitational field at a distance of 2.5r from centre is 825Gmr2CThe gravitational field at a distance of 1.5r from centre is zeroDThe gravitational field between the sphere and spherical shell is uniform.A solid sphere of radius a and mass m is surrounded by cocentric spherical shell of thickness 2a and mass 2m the gravitational field at a distance 3a from their centres is
AGma2BGm3a2CGm5a2DGm4a2A particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
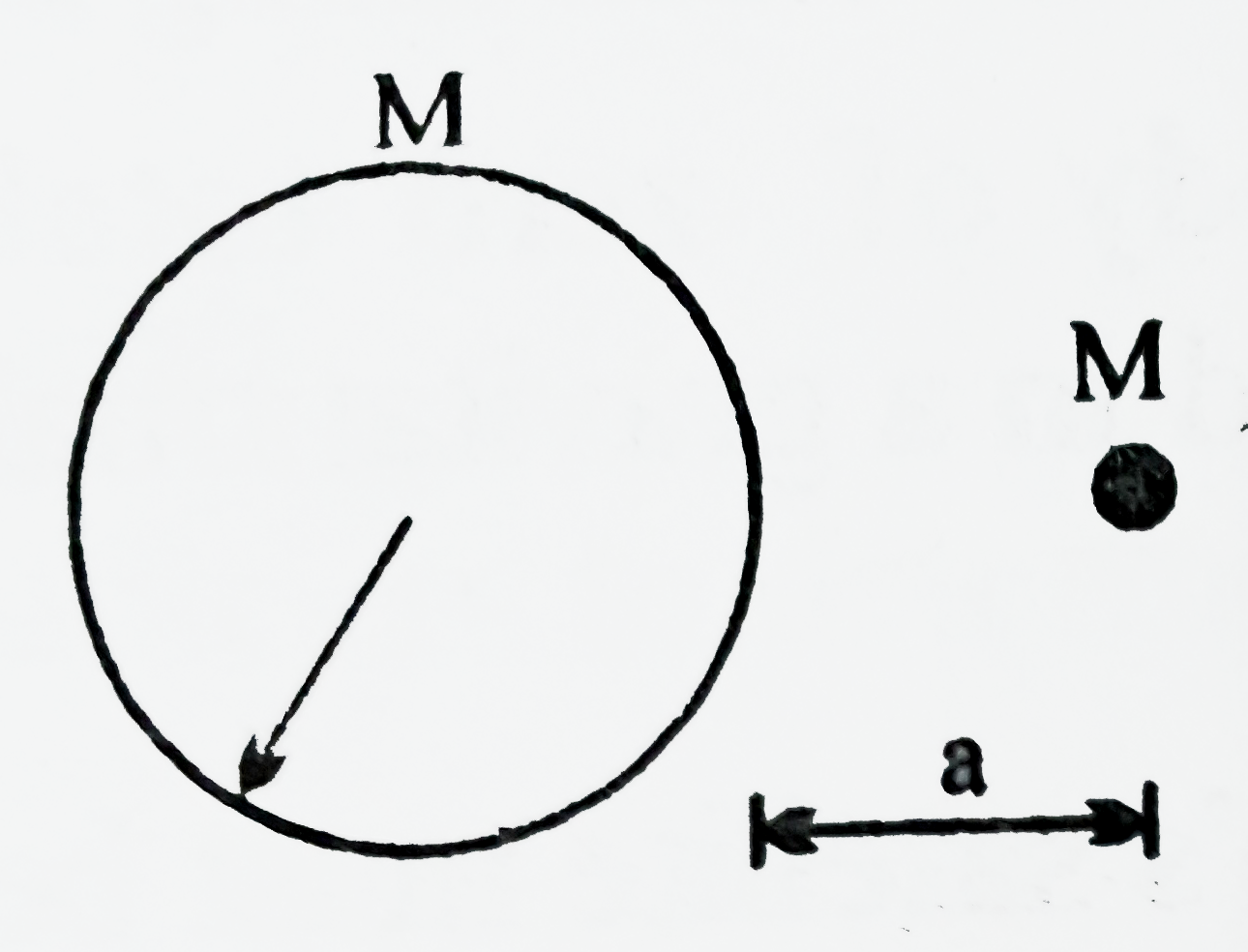 AGravitational field and potential both are zero at centre of the shell.BGravitational field is zero not only inside the shell but at a point outside the shell also.CInside the shell, gravitational field alone is zeroDNeither gravitational field nor gravitational potential is zero inside the shell.
AGravitational field and potential both are zero at centre of the shell.BGravitational field is zero not only inside the shell but at a point outside the shell also.CInside the shell, gravitational field alone is zeroDNeither gravitational field nor gravitational potential is zero inside the shell.
A solid sphere of mass M and radius R is surrounded by a concentric shell of equal mass M and radius 3R. The gravitational field at a point P1 at a distance r1=2R from the centre is I1 and a point P2at distance r2=4R from the centre is I2 The ratio I2I1
View SolutionFor a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
View SolutionA uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
View SolutionA particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
View SolutionConsider a thin spherical shell of uniform density of mass M and radius R:
View Solution
