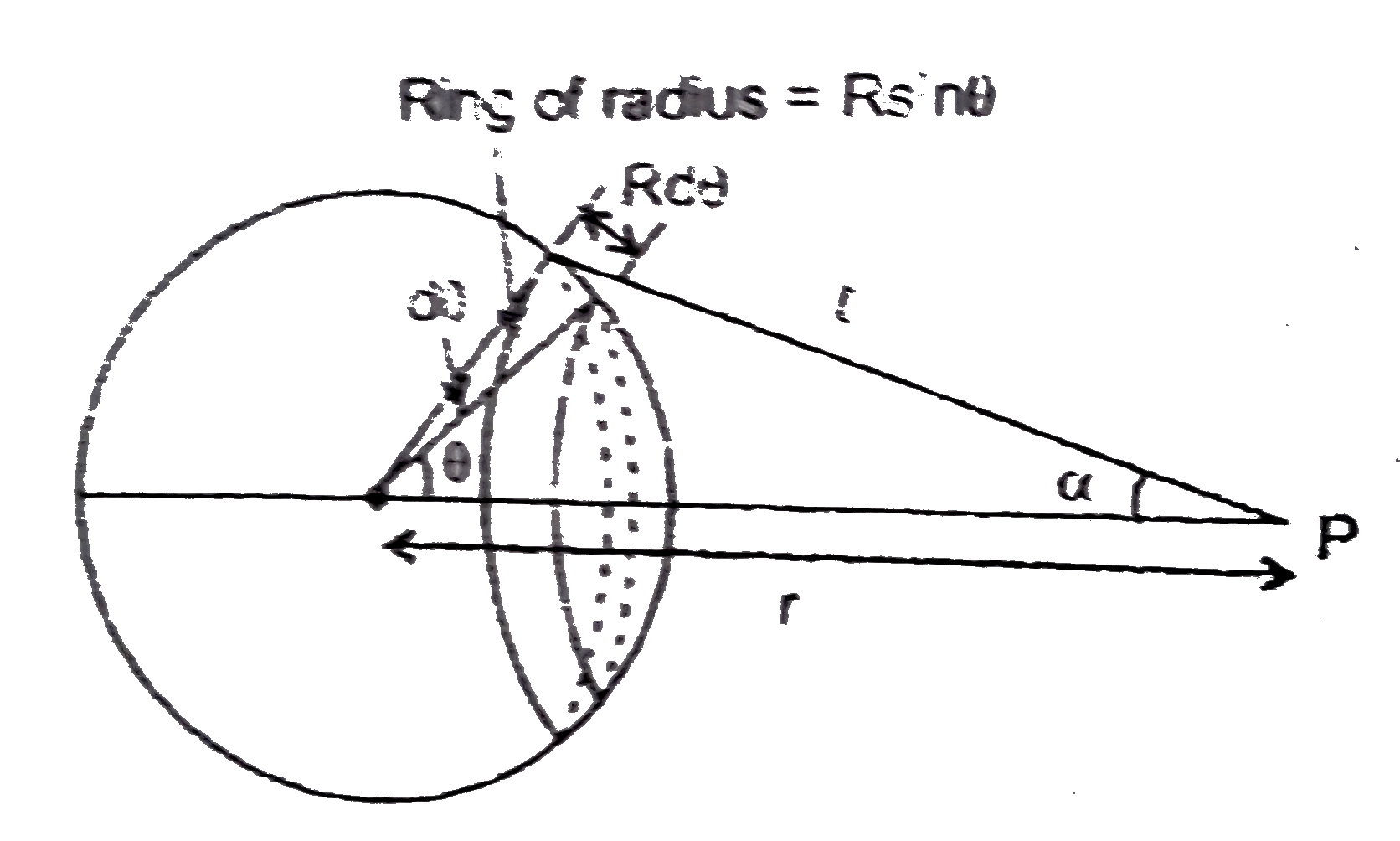
For a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
dE=GdMl2cosα ≥R
dM=M4πR2×2πRsinθRdθ
dM=M2sinθdθ
∴dE=Gmsinθcosαdθ2l2
Now l2=R2+r2−2rRcosθ....(1)
R2=l2+r2−2lrcosα...(2)
∴cosα=l2+r2−R22lr
cosθ=R2+r2−l22rR
differentiating (1)
∴2ldl=2rRsinθdθ
∴dE=GM2l2.ldlRr.l2+r2−R2(2lr)⇒dE=GM4Rr2[1+r2−R2l2]dl
∴E=∫dE=GM4Rr2[∫r+Rr−Rdl+(r2dl−R2)∫r+Rr−Rdll2]
⇒E=GMr2r≥R
If point is inside the shell limit changes to [(R -r) to R +r]
E=0 where r<R
 .
.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - SOLVED MISCELLANEOUS PROBLEMS5videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXAMPLE2videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions16videos
NUCLEAR PHYSICS
Similar Questions
A solid shere of mass m and radius r is placed inside a hollow spherical shell of mass 4m and radius 4r find gravitational field intensity at
(a) r<y<2r (b) 2r<y<8r (c) y>8r
here coordinate is measured from the point of contact of the sphere and the shell
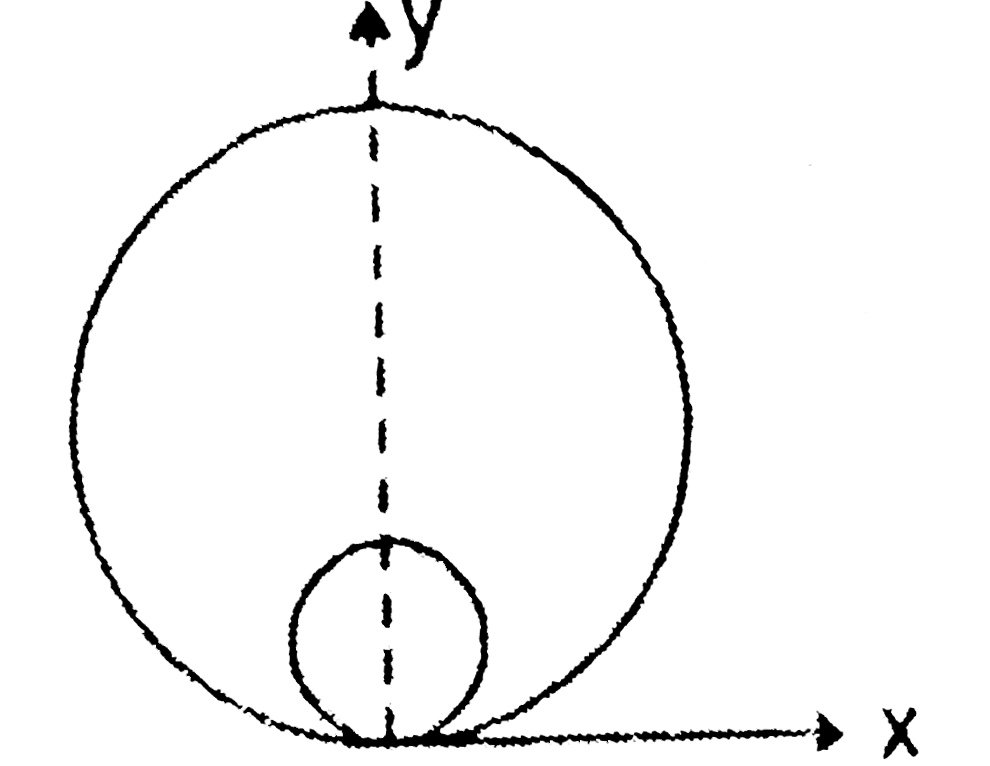 .View Solution
.View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
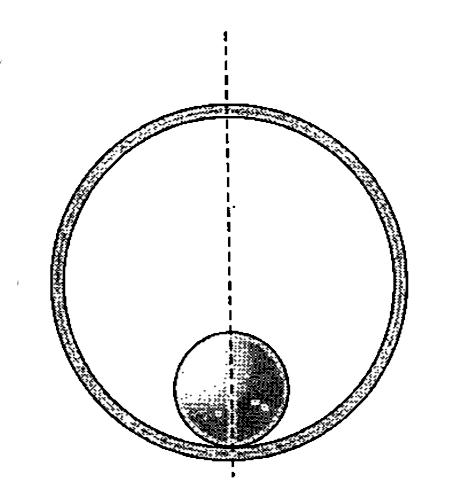 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Consider a thin spherical shell of uniform density of mass M and radius R:
AThe gravitational field inside the shell will be zeroBThe gravitational self energy of shell is GM22RCAttractive force experience by unit area of the shell pull the other half is GM22R2DNet gravitational force with which one hemisphere of the shell arracts other, is GM28R2 - Question 2 - Select One
Consider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
A−GM2RB−12GM2RC−35GM2RD−23GM2R - Question 3 - Select One
A shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
A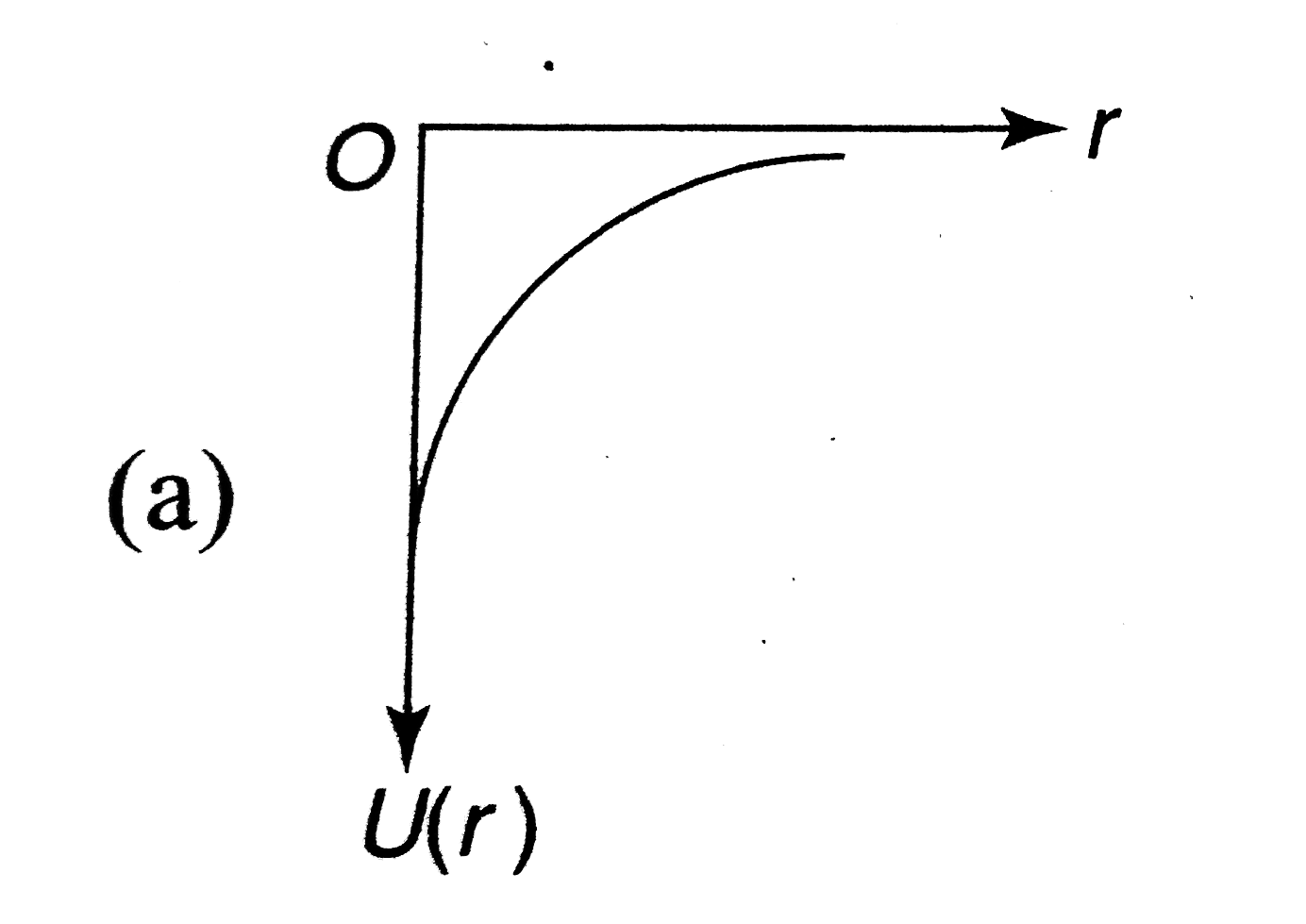 B
B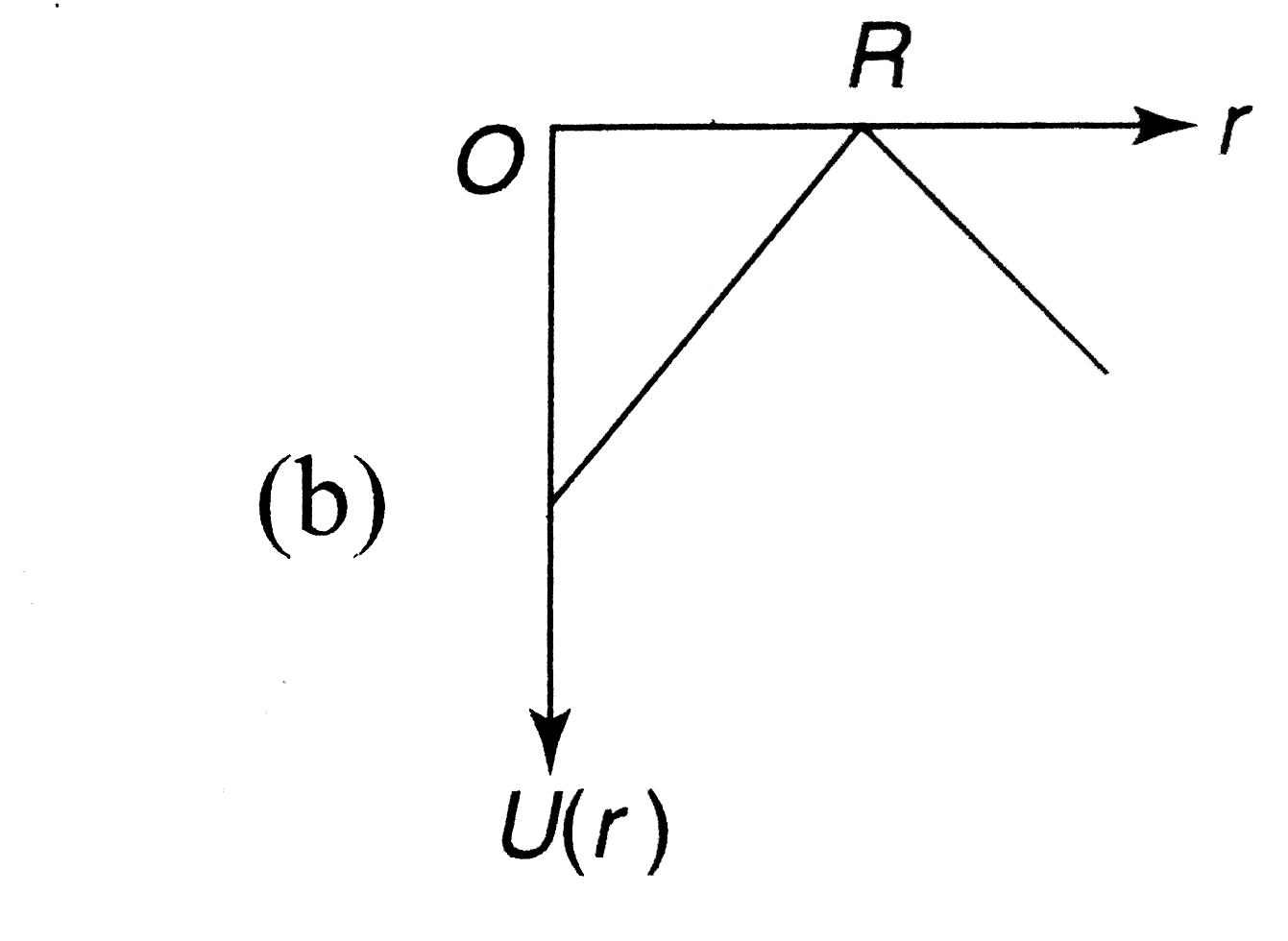 C
C D
D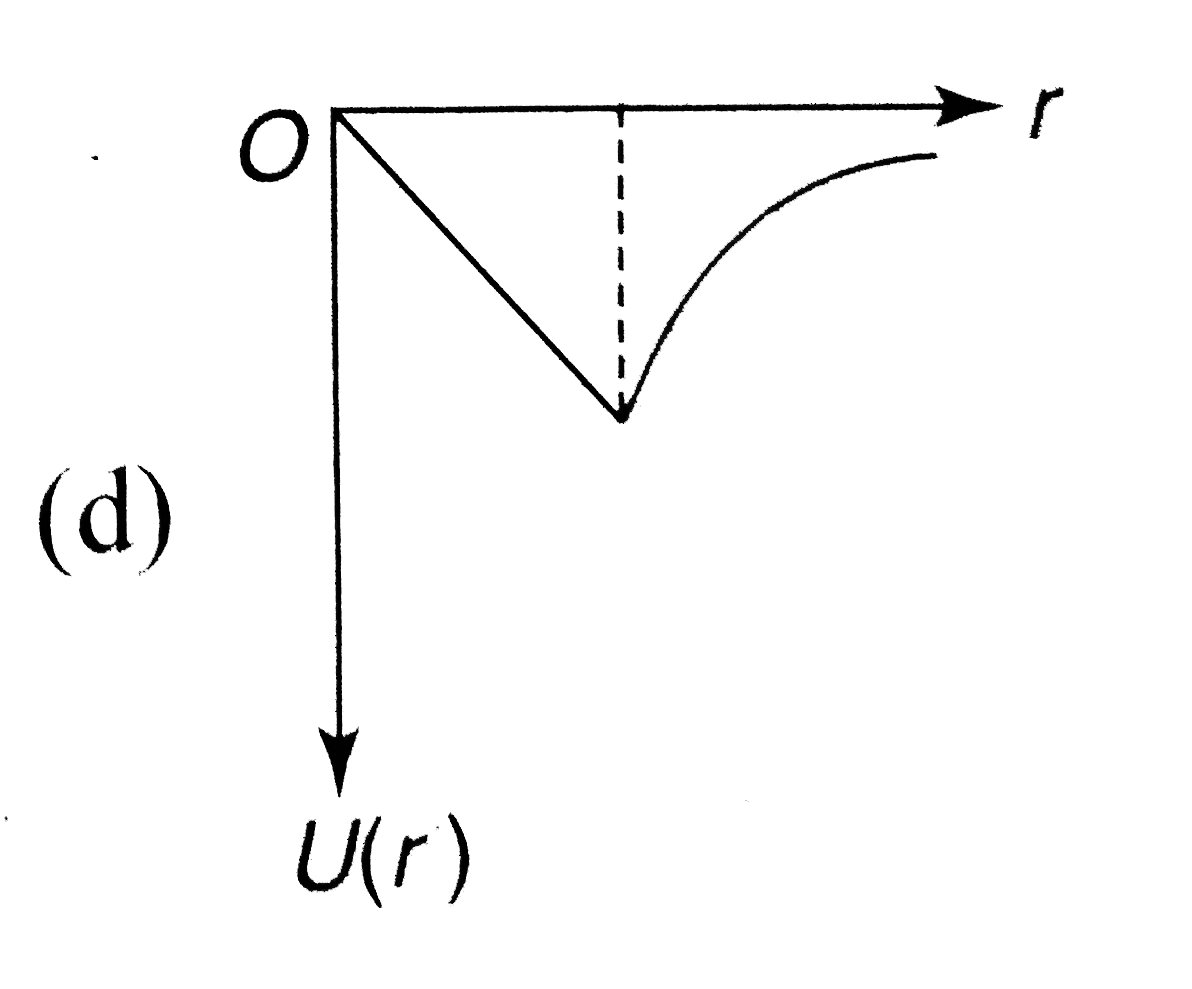
Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 View Solution
View SolutionIn a spherical region the densiy varies inversely with the distance from ther centre Gravitational field at a distance r from the centre is .
View Solution

