A uniform sphere of mass M and radius R exerts a force F on a small mass m situated at a distance of 2R from
the centre O of the sphere. A spherical portion of diameter R is cut from the sphere as shown in Fig. The force
of attraction between the remaining part of the sphere and the mass m will be
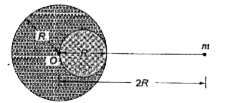
7F9
2F3
4F9
F3
The correct Answer is:A
The force of attraction between the complete sphere and mass m is
F=GmM(2R)2=GmM4R2 .......(i)
Mass of complete sphere is M=4π3R3ρ.
Mass of the cut out portion is m0=4π3(R2)3ρ.
Thus, m0=M8 . The distance between the centre of the cut out portion and mass m = 2R- R2=3R2.
Hence the force of attraction between the cut out portion and mass m is
f=Gm0m(3R/2)2=G(M/8)m9R2/4=GmM4R2×29
Using (i), we get f=2F9. There fore, the force of attraction between the remaining part of the sphere
and mass m = F-f=F- 2F9=7F9
Similar Questions
The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionFind the force of attraction between a solid sphere of mass M and a ring of mass m as shown.
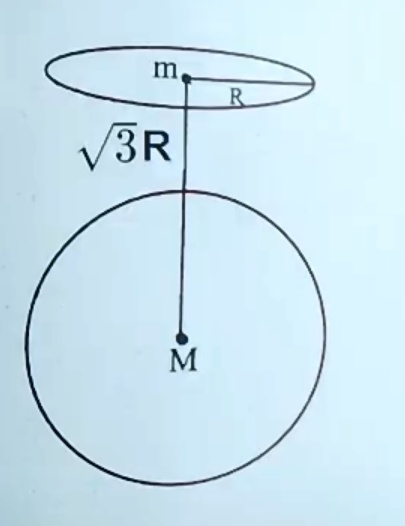
View Solution
Knowledge Check
The centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance √8R apart as shown. The force of attraction between the ring and the sphere is
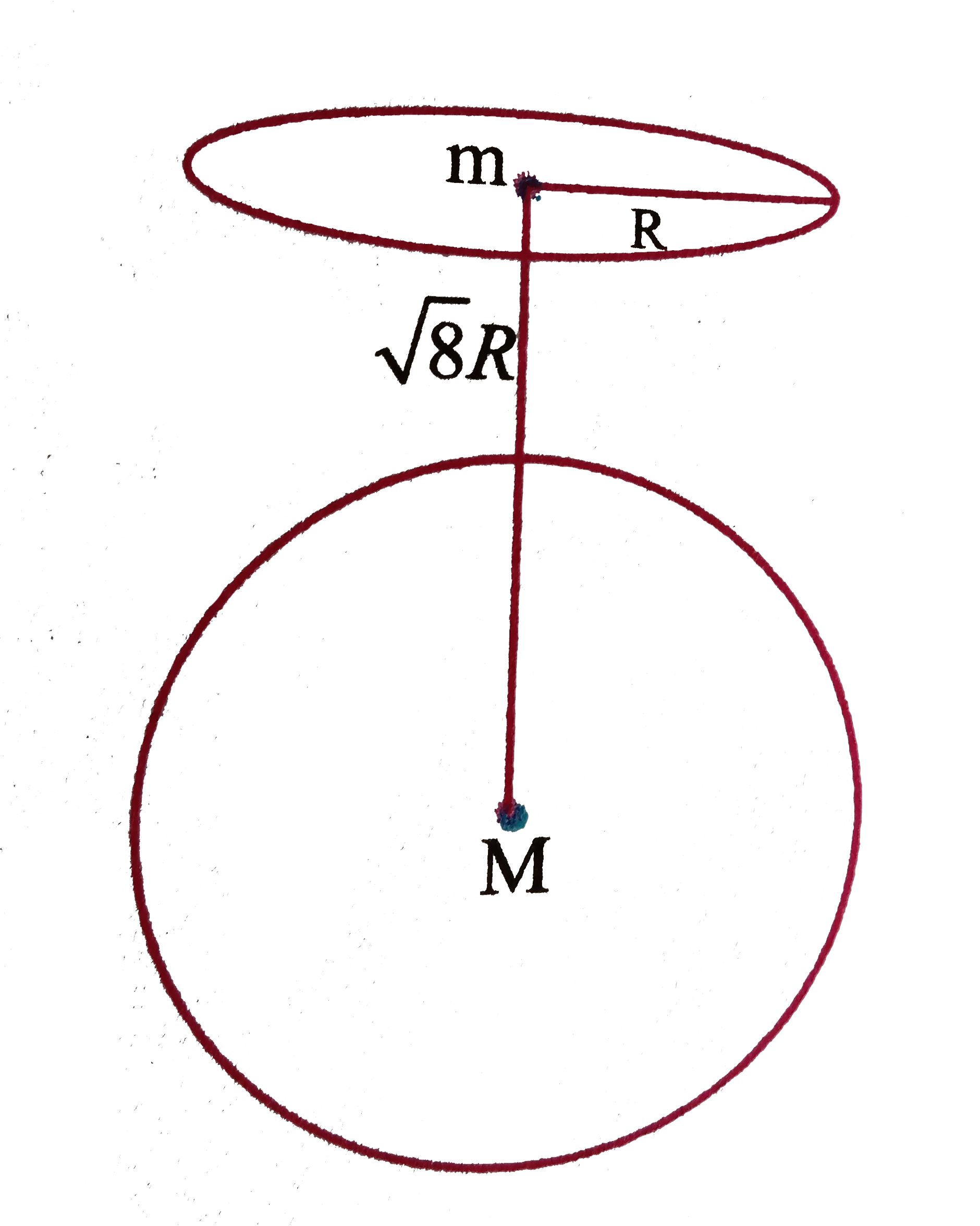 A2√227GmMR2BGmM8R2CGmM9R2D√29GmM9R2
A2√227GmMR2BGmM8R2CGmM9R2D√29GmM9R2The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of theseA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
A8GM2R2B2GM2√3R2C3GM22R2D√32GM2R2
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
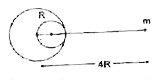
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ

View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
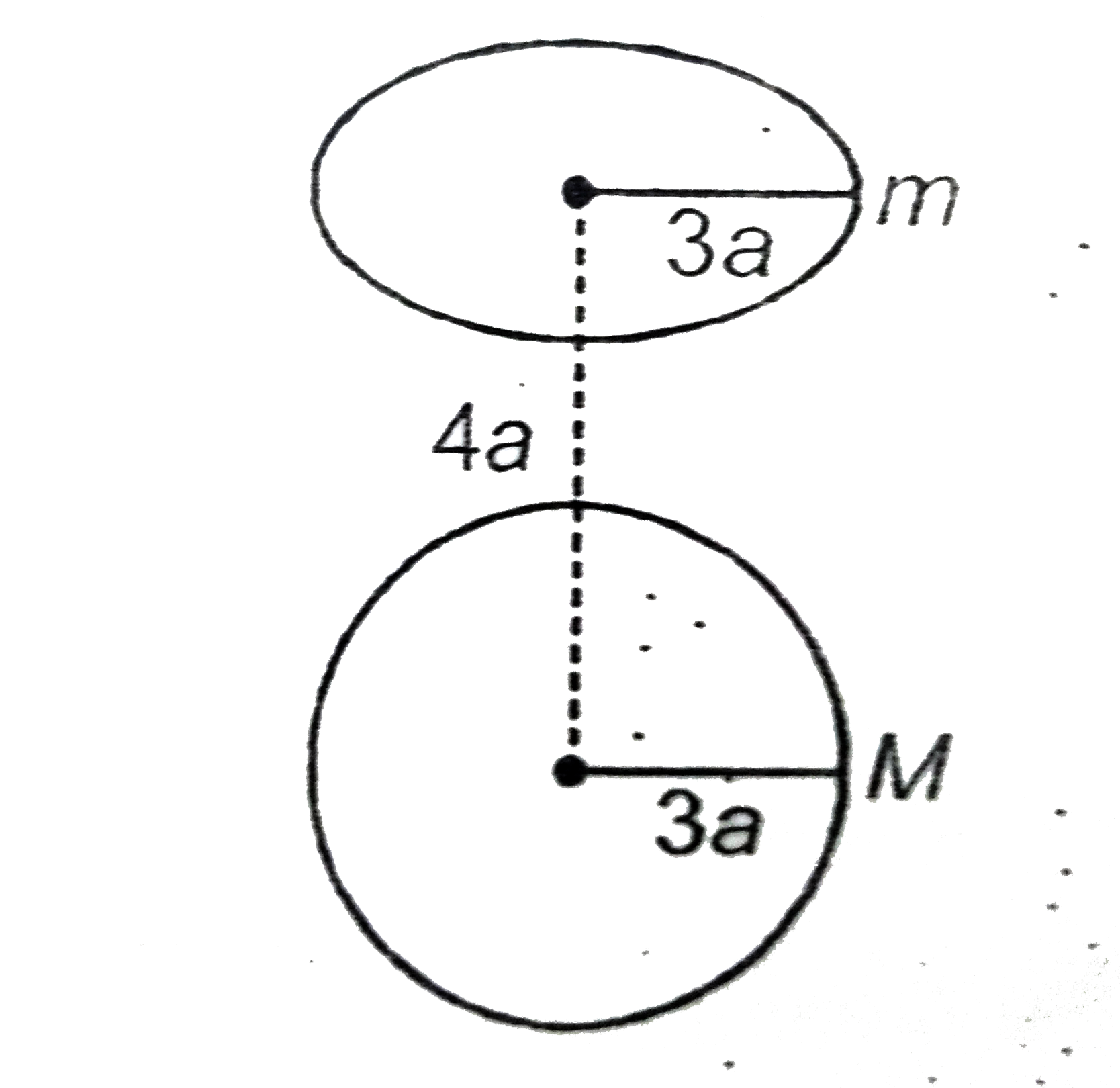
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
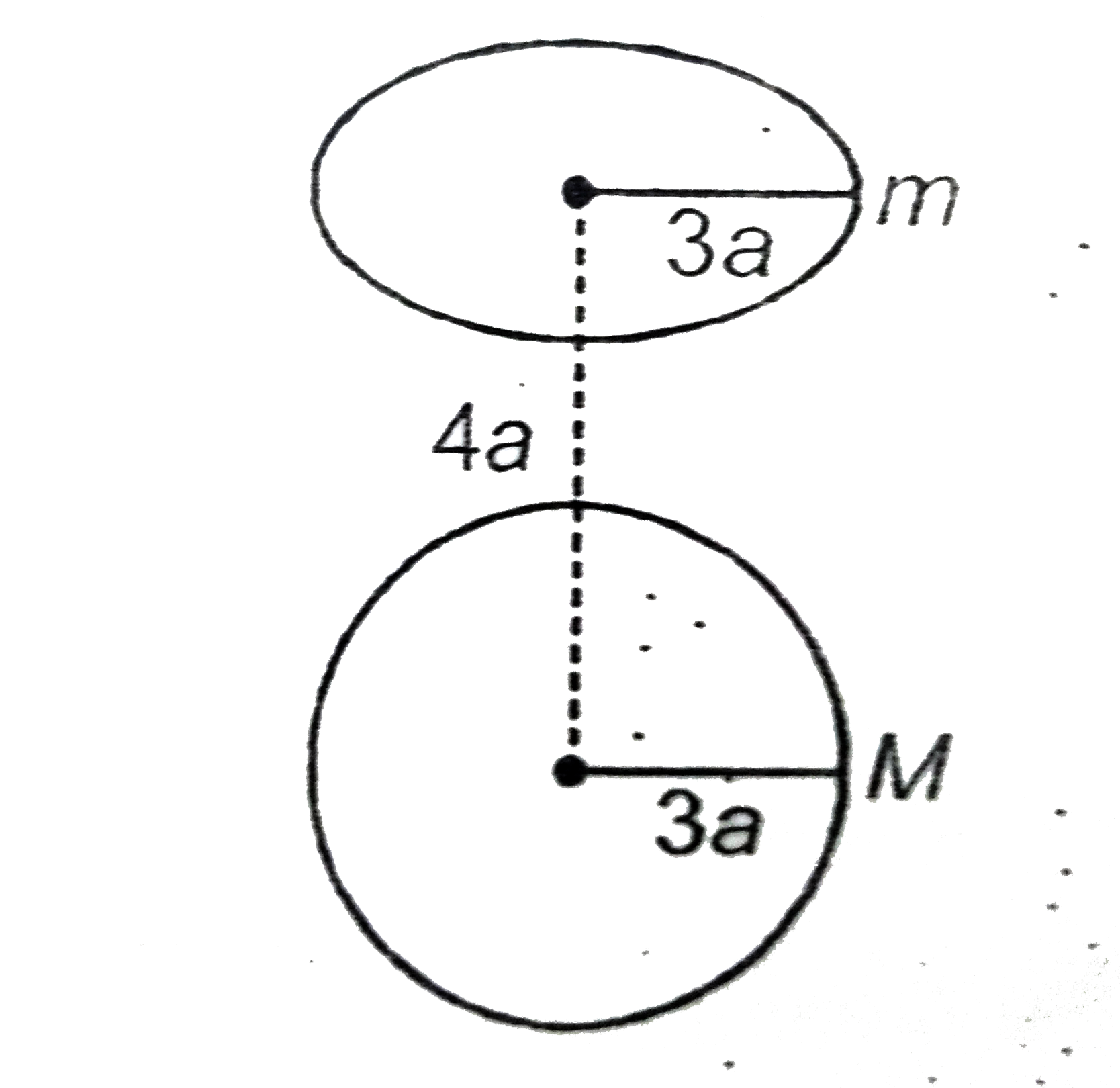
View SolutionA uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is

View Solution
