A uniform sphere of mass $m$ and radius $r$ rolls without sliding over a horizontal plane, rotating ahout a horizontal axle $O A$ . In the process, the centre of the sphere moves with a veocity $v$ along a circle of radius $R$ . Find the kinetic energy of the sphere.

Video Solution

Text Solution

Verified by Experts

Here the motion of the body is oribital and spin combined. The sphere is spining about a horizontal axis and orbiting about a vertical axis.
We write total kinetic energy of the sphere i.e.,
$K E = K_{orbital} + K_{spin}$

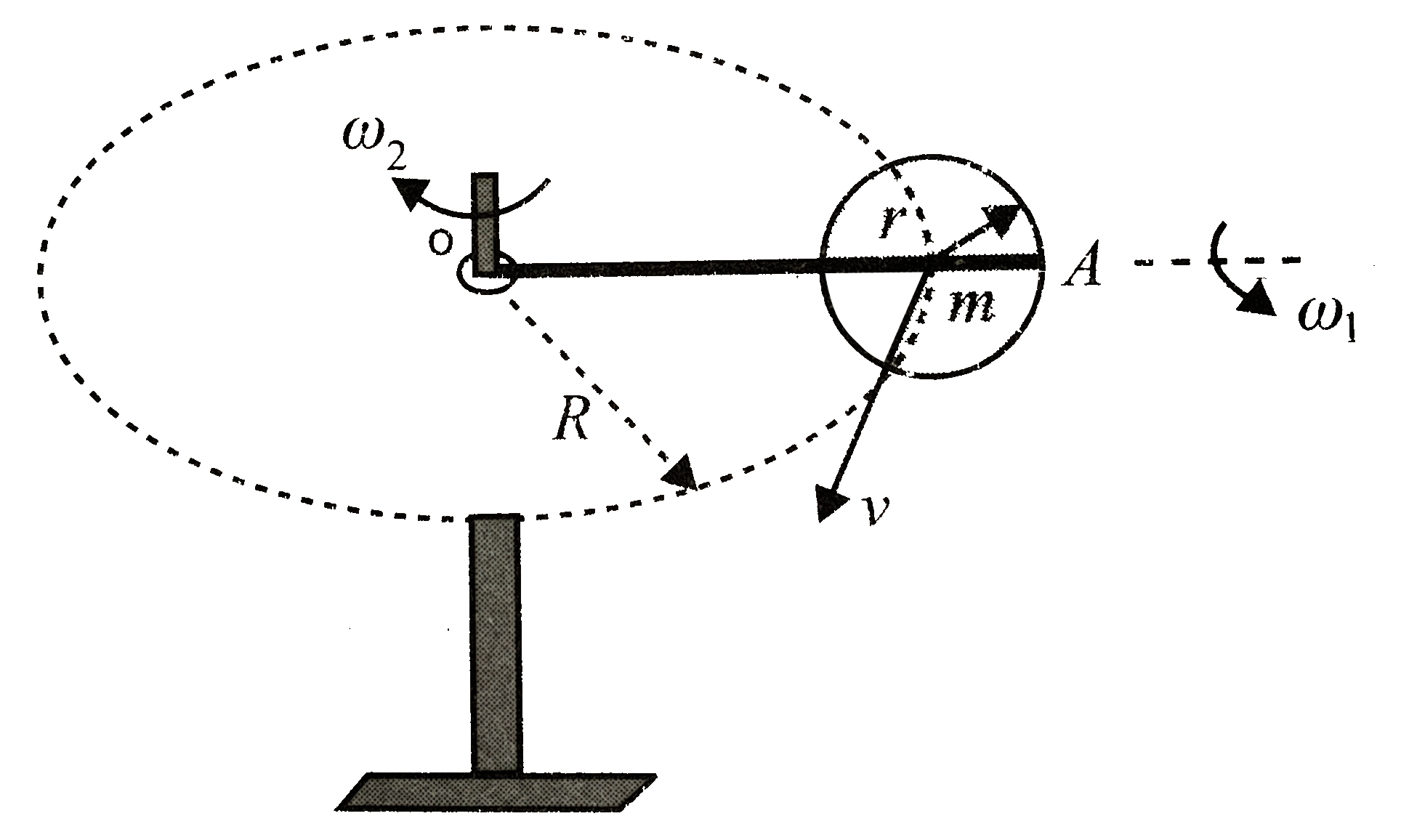
The kinetic energy of the sphere due to its rotation about its own axis nad its motion along circular path with velocity $v$ .
$K E = \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2}$
where $I_{1} = \frac{2}{5} m r^{2}$ and $I_{2} = (\frac{2}{5} m r^{2} + m R^{2})$
$ω_{1} = \frac{v}{r}$ and $ω_{2} = \frac{v}{R}$
Substituting these values in the above equation, we get
$K E = \frac{7 m}{10} v^{2} [1 + \frac{2 r^{2}}{7 R^{2}}]$

Updated on:21/07/2023

A solid sphere of mass $m$ and radius $R$ rolls without slipping on a horizontal surface such that $v_{c . m .} = v_{0}$ .
AThe kinetic energy of rotation is $\frac{1}{5} m v_{0}^{2}$ .
BThe total kinetic energy is $\frac{7}{10} m v_{0}^{2}$ .
CThe mechanical energy (assume the ground as reference) is $m g R + \frac{7}{10} m v_{0}^{2}$ .
DAll options are correct.
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
A0.014 J
B0.028 J
C14 J
D28 J
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
A0.014 J
B0.028 J
C14 J
D28 J