A uniform steel bar of cross-sectional area A and length L is suspended, so that it hangs vertically. The stress at the middle point of the bar is (ρ is the density of stell)
L2Aρg
Lρg2
LAρg
Lρg
The correct Answer is:b
To find the stress at the middle point of a uniform steel bar of cross-sectional area A and length L that is suspended vertically, we can follow these steps:
Step 1: Understand the Concept of Stress
Stress is defined as the force applied per unit area. Mathematically, it is expressed as:
Stress=ForceArea
Step 2: Identify the Force at the Midpoint
When the bar is suspended, the force acting on the midpoint is due to the weight of the lower half of the bar. The weight of an object is given by:
Weight=mass×g
where g is the acceleration due to gravity.
Step 3: Calculate the Mass of the Lower Half of the Bar
The mass of the entire bar can be expressed in terms of its density ρ and volume. The volume V of the bar is given by:
V=A×L
Thus, the mass m of the entire bar is:
m=ρ×V=ρ×A×L
The mass of the lower half of the bar is:
mlower=m2=ρ×A×L2
Step 4: Calculate the Force at the Midpoint
The force acting at the midpoint due to the weight of the lower half of the bar is:
F=mlower×g=(ρ×A×L2)×g=ρ×A×L×g2
Step 5: Substitute into the Stress Formula
Now, we can substitute the force F into the stress formula:
Stress=FA=ρ×A×L×g2A
Step 6: Simplify the Expression
The area A cancels out:
Stress=ρ×L×g2
Final Answer
Thus, the stress at the midpoint of the bar is:
Stress=ρ×L×g2
Stress is defined as the force applied per unit area. Mathematically, it is expressed as:
Stress=ForceArea
When the bar is suspended, the force acting on the midpoint is due to the weight of the lower half of the bar. The weight of an object is given by:
Weight=mass×g
where g is the acceleration due to gravity.
The mass of the entire bar can be expressed in terms of its density ρ and volume. The volume V of the bar is given by:
V=A×L
Thus, the mass m of the entire bar is:
m=ρ×V=ρ×A×L
The mass of the lower half of the bar is:
mlower=m2=ρ×A×L2
The force acting at the midpoint due to the weight of the lower half of the bar is:
F=mlower×g=(ρ×A×L2)×g=ρ×A×L×g2
Now, we can substitute the force F into the stress formula:
Stress=FA=ρ×A×L×g2A
The area A cancels out:
Stress=ρ×L×g2
Thus, the stress at the midpoint of the bar is:
Stress=ρ×L×g2
Topper's Solved these Questions
- ELASTICITY BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - MHT CET CORNER
16 Videos
- ELASTICITY BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - EXERCISE 1
66 Videos
- CURRENT ELECTRICITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - MHT CET CONER
34 Videos
Similar Questions
One end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
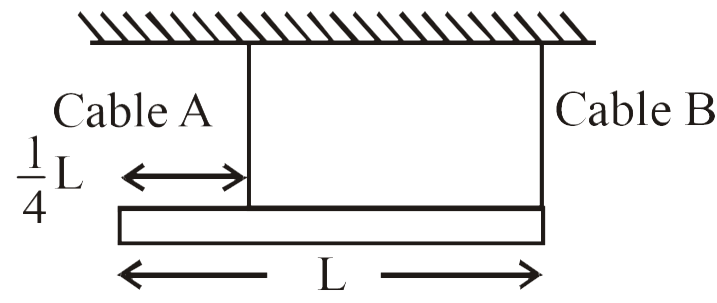
View Solution
Knowledge Check
A uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
A12ρgLB14ρgLCρgLDNone of theseA steel bar of cross-sectional area A and length l is magnetised to develop an intensity of magnetisation l . The pole strength of the bar is
AIABIlACIlD1IAA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equlibrium is:
A(a) MgkB(b) Mgk(1−LAσM)C(c) Mgk(1−LAσ2M)D(d) Mgk(1+LAσM)
A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionA unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
View SolutionOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionA steel rod of length L, density d and cross-sectional area A, is hinged at one end so that it can rotate freely in a vertical plane. The rod is released from a horizontal position. When it becomes vertical, the stress at its midpoint is
View Solution
