A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
12π(k−AρgM)1/2
12π(k+AρgM)1/2
12π(k+ρgLM)1/2
(1)/(2 pi) ((k + A rho g)/(A rho g))^(1//2)
The correct Answer is:B
If (x) is the displacement then,
:. Mω2x=[ρAg+k]x
⇒ω=[ρAg+km]1/2⇒v=12π[ρAg+kM]1/2.
Topper's Solved these Questions
Similar Questions
A uniform cylinder of height h, mass m and cross sectional area A is suspended vertically from a fixed point by a massless spring of force constant k, A beaker full of water is placed under the cylinder so that 1/4th of its volume is submerged in the water at equilibrium position. When the cylinder is given a small downward push and released, it starts oscillating vertically with small amplitude. Calculate the frequency of oscillation of the cylinder, Take, density of water =ρ.
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View Solution
Knowledge Check
A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density σ at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period T of the oscillations of the cylinder will be :
ASmaller than 2π[M(k+Aσg)]12B2π√MkCLarger than 2π[M(k+Aσg)]12D2π[M(k+Aσg)]12A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equlibrium is:
A(a) MgkB(b) Mgk(1−LAσM)C(c) Mgk(1−LAσ2M)D(d) Mgk(1+LAσM)A uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

If the cyleinder is displced by a small downward displacement a from its equilibrium postion and then released , the restoring force on it will beA−[K+Apg]a4B−[K+14Apg]aC−[K−14Apg]aD−[K+Apg]a
A uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffness, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

The elongation X0 produced in the springs when the syste is in equilibrium is
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

Time period of vertical S.H.M of the cylinder is
View SolutionA uniform steel bar of cross-sectional area A and length L is suspended, so that it hangs vertically. The stress at the middle point of the bar is (ρ is the density of stell)
View SolutionA uniform cylinder of mass m and radius R is in equilibrium on an inclined plane by the action of a light spring of stiffness k, gravity and reaction force acting on it. If the angle of inclination of the plane is ϕ, then angular frequency of small oscillations of the cylinder is...........
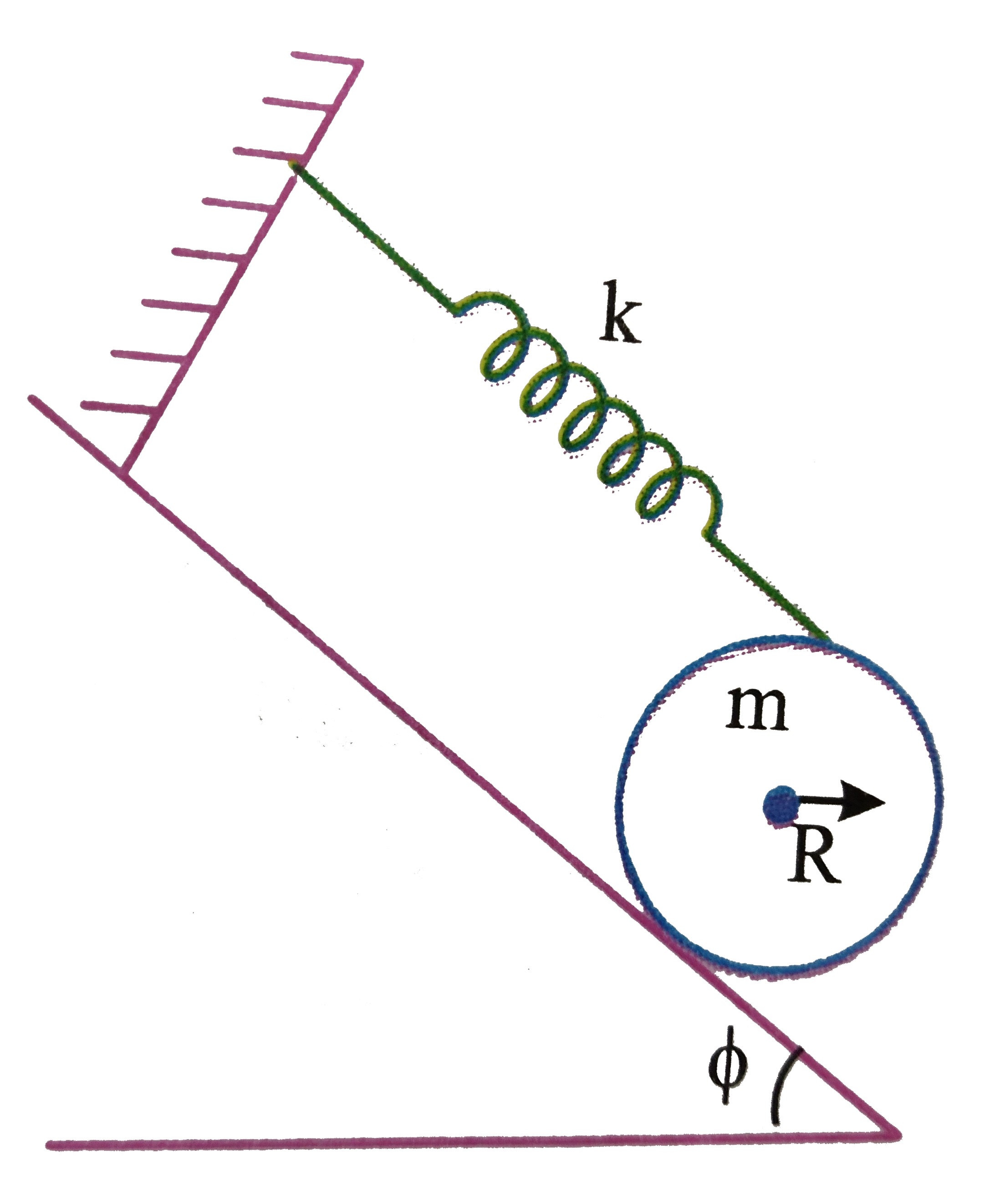
View Solution
