A uniform wire of resistance R is shaped into a regular n−sided polygon (n is even), The equivalent resistance between any two corners can have.
(i) the maximum value R4
(ii) the minimum value Rn
(iii) the minimum value R(n−1n2)
(iv) the minimum value Rn.
(i),(ii)
(i),(iii)
(i) only
(i),(iv)
The correct Answer is:B
To solve the problem of finding the equivalent resistance between any two corners of a uniform wire shaped into a regular n-sided polygon (where n is even), we will analyze the configuration step by step.
Step 1: Understanding the Configuration
We have a uniform wire of resistance R shaped into a regular n-sided polygon. Since n is even, we can visualize the polygon as having equal sides, with each side having a resistance of Rn.
Hint: Remember that the total resistance of the wire is distributed evenly across the n sides.
Step 2: Maximum Resistance Calculation
To find the maximum equivalent resistance between any two corners, we consider the case when n=2 (the simplest polygon, a straight line). In this case, the resistance between the two corners is simply the sum of the two halves of the wire:
Rmax=R2+R2=R
However, since we are looking for the equivalent resistance between two adjacent corners in a polygon with more sides, we can find that the maximum resistance occurs when the two corners are directly connected through the wire, leading to:
Rmax=R4
Hint: The maximum occurs when the two corners are adjacent, and the total resistance is divided among the paths available.
Step 3: Minimum Resistance Calculation
To find the minimum equivalent resistance, we consider the case where the two corners are opposite each other in the polygon. For a regular n-sided polygon, the equivalent resistance between two opposite corners can be calculated as follows:
1. Each side has a resistance of Rn.
2. The two corners are connected through n−1 sides in parallel.
The equivalent resistance Rmin can be calculated using the formula for resistors in parallel:
Rmin=R/nn−1=R(n−1)n2
Hint: When calculating minimum resistance, consider the paths available and how they combine in parallel.
Step 4: Summary of Results
From our calculations, we can summarize:
- The maximum equivalent resistance between any two corners is R4.
- The minimum equivalent resistance between any two corners is R(n−1)n2.
Conclusion
Based on our analysis, the correct statements regarding the equivalent resistance between any two corners of the n-sided polygon are:
- (i) The maximum value is R4 - Correct
- (ii) The minimum value is Rn - Incorrect
- (iii) The minimum value is R(n−1)n2 - Correct
- (iv) The minimum value is Rn - Incorrect
Thus, the correct options are (i) and (iii).
We have a uniform wire of resistance R shaped into a regular n-sided polygon. Since n is even, we can visualize the polygon as having equal sides, with each side having a resistance of Rn.
To find the maximum equivalent resistance between any two corners, we consider the case when n=2 (the simplest polygon, a straight line). In this case, the resistance between the two corners is simply the sum of the two halves of the wire:
To find the minimum equivalent resistance, we consider the case where the two corners are opposite each other in the polygon. For a regular n-sided polygon, the equivalent resistance between two opposite corners can be calculated as follows:
2. The two corners are connected through n−1 sides in parallel.
From our calculations, we can summarize:
- The minimum equivalent resistance between any two corners is R(n−1)n2.
Based on our analysis, the correct statements regarding the equivalent resistance between any two corners of the n-sided polygon are:
- (i) The maximum value is R4 - Correct
- (ii) The minimum value is Rn - Incorrect
- (iii) The minimum value is R(n−1)n2 - Correct
- (iv) The minimum value is Rn - Incorrect
Topper's Solved these Questions
Similar Questions
Knowledge Check
A uniform wire of resistance R is slaped into a regular n-sided polygon (n is seven). The equivalent resistance between any two corners can have :
Athe maximum value R/4Bthe maximum value R/nCthe minimum value R(n−1n2)Dthe minimum value R/nThree equal resistances each of value R are joined as shown in the figure. The equivalent resistance between M and N is
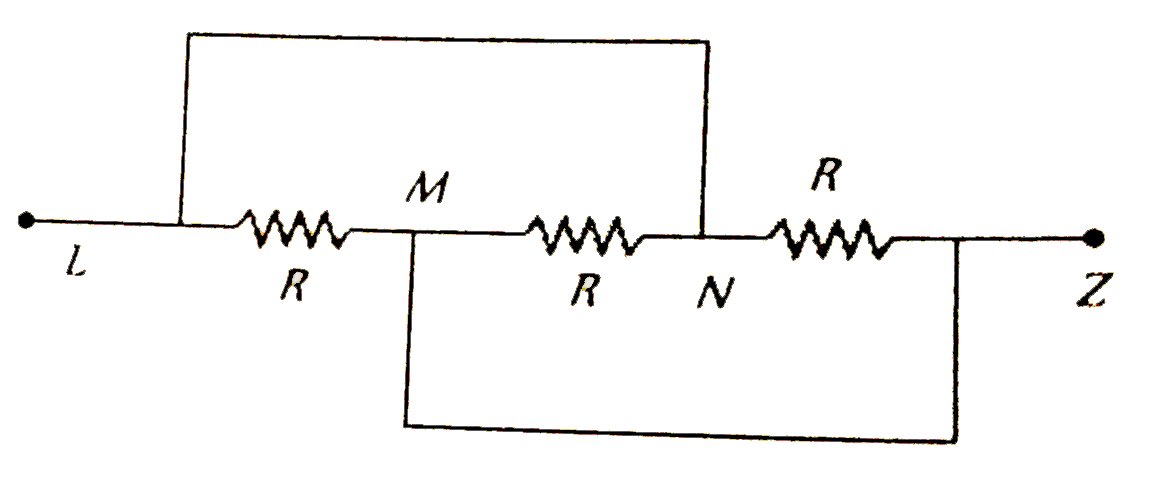 ARB2RCR2DR3
ARB2RCR2DR3If r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
Aa2cot(π2n)Ba2cot(πn)Ca2tan(πn)Da2cos(πn)
If n(A)=5 and n(B)=8, then the sum of the mini-mum value of n(A∩B) and the maximum value of n(A∪B) is ____.
View SolutionFind the value of n!(n−r)!,if n=10 and r=3.
View SolutionIf n resistors each of resistance r are connected to get (i) maximum possible resistance (ii) minimum possible resistance. Compute the ratio between values of resistances obtained in (i) and (ii).
View SolutionIf R is the radius of circumscribing circle of a regular polygon of n-sides,then R =
View SolutionWe have n resistors each of resistance R. The ratio of the combination for maximum and minimum values is
View Solution
