We have n resistors each of resistance R. The ratio of the combination for maximum and minimum values is
n
n2
n3
1n
The correct Answer is:B
To find the ratio of the maximum and minimum resistance values when combining n resistors each of resistance R, we can follow these steps:
Step 1: Calculate Maximum Resistance
The maximum resistance occurs when all resistors are connected in series. The formula for the equivalent resistance Req in series is:
Req=R1+R2+R3+…+Rn
Since each resistor has the same resistance R:
Req=R+R+R+…+R(n times)=nR
Thus, the maximum resistance Rmax is:
Rmax=nR
Step 2: Calculate Minimum Resistance
The minimum resistance occurs when all resistors are connected in parallel. The formula for the equivalent resistance Req in parallel is:
1Req=1R1+1R2+1R3+…+1Rn
Again, since each resistor has the same resistance R:
1Req=1R+1R+1R+…+1R(n times)=nR
Thus, the equivalent resistance Req is:
Req=Rn
So, the minimum resistance Rmin is:
Rmin=Rn
Step 3: Calculate the Ratio of Maximum to Minimum Resistance
Now, we find the ratio of the maximum resistance to the minimum resistance:
Ratio=RmaxRmin=nRRn=nR⋅nR=n2
Final Answer
Thus, the ratio of the combination for maximum and minimum values is:
Ratio=n2
The maximum resistance occurs when all resistors are connected in series. The formula for the equivalent resistance Req in series is:
Req=R1+R2+R3+…+Rn
Since each resistor has the same resistance R:
Req=R+R+R+…+R(n times)=nR
Thus, the maximum resistance Rmax is:
Rmax=nR
The minimum resistance occurs when all resistors are connected in parallel. The formula for the equivalent resistance Req in parallel is:
1Req=1R1+1R2+1R3+…+1Rn
Again, since each resistor has the same resistance R:
1Req=1R+1R+1R+…+1R(n times)=nR
Thus, the equivalent resistance Req is:
Req=Rn
So, the minimum resistance Rmin is:
Rmin=Rn
Now, we find the ratio of the maximum resistance to the minimum resistance:
Ratio=RmaxRmin=nRRn=nR⋅nR=n2
Thus, the ratio of the combination for maximum and minimum values is:
Ratio=n2
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MISCELLANEOUS QUESTIONSEXERCISE - PART-B99videos
MISCELLANEOUS QUESTIONS
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)13videos
MEASUREMENT
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MOTIONEXERCISE - HIGHER ORDER THINKING QUESTIONS48videos
MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
n resistors each of resistance R first combine to give maximum effective resistgance and then combine to give minimum. The ratio of the maximum resistance is
AnBn2Cn2−1Dn3
Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
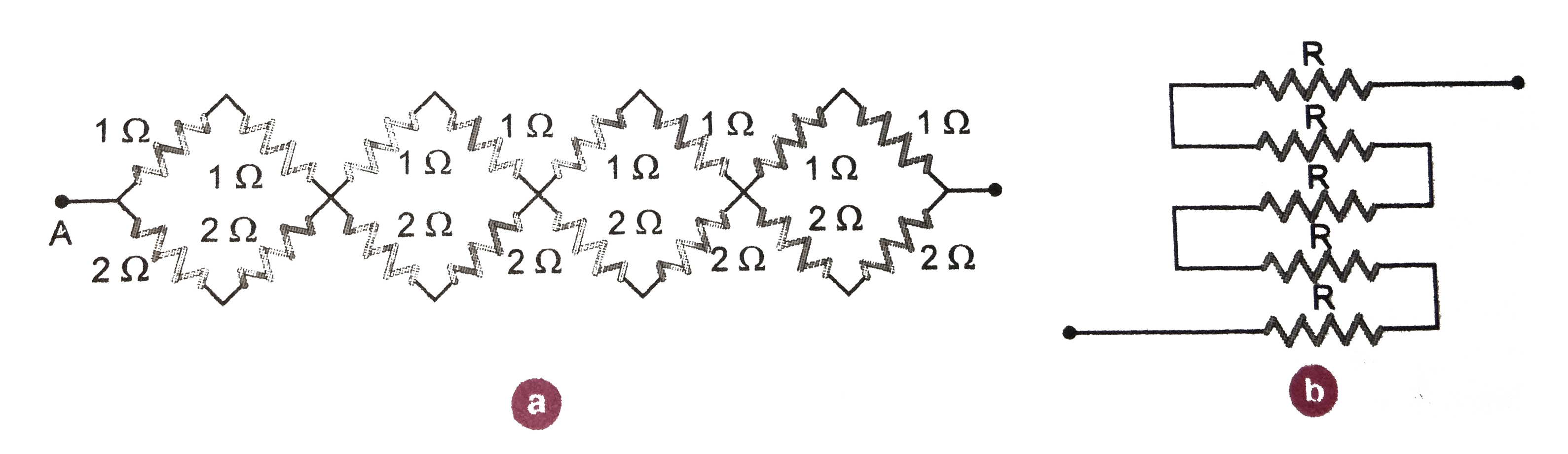 View Solution
View SolutionGiven n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View SolutionYou are given n resistors each of resistance r .These are first connected to get minimum resistance .In the secoind case these are again connected differently to get maximum possible resistance. Compute the ratio between the minimum and maximum value of resistance so obtained.
View SolutionYou are given 10 resistors each of resistance 2Ω. First they are connected to obtain possible minimum resistance. Then they are connected to obtain possible maximum resistance. The ratio of maximum and minimum resistance is ________________ .
View SolutionWhy is resistance more in series combination of resistors ?
View SolutionIf n resistors each of resistance r are connected to get (i) maximum possible resistance (ii) minimum possible resistance. Compute the ratio between values of resistances obtained in (i) and (ii).
View Solution

