A uniformly charged sphere has charge Q. An electron (charge – e, mass m) revolves around it in a circular orbit of radius r. (a) Write the total energy (i.e., sum of its kinetic energy and electrostatic potential energy in the field of the sphere) of the electron. (b) If the time period of revolution of the electron in circular orbit of radius r is T, then find the time period if the orbital radius is made 4r.
The correct Answer is:(a).
(b). 8T
Step by step video, text & image solution for A uniformly charged sphere has charge Q. An electron (charge – e, mass m) revolves around it in a circular orbit of radius r. (a) Write the total energy (i.e., sum of its kinetic energy and electrostatic potential energy in the field of the sphere) of the electron. (b) If the time period of revolution of the electron in circular orbit of radius r is T, then find the time period if the orbital radius is made 4r. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 2
77 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
Two unequal masses, m1=2m and m2=m have unequal positive charge on them. They are suspended by two mass-less threads of unequal lengths from a common point such that, in equilibrium, both the masses are on same horizontal level. The angle between the two strings is θ=45∘ in this position. Find the Electrostatic force applied by m1 on m2 in this position.

View SolutionThree small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
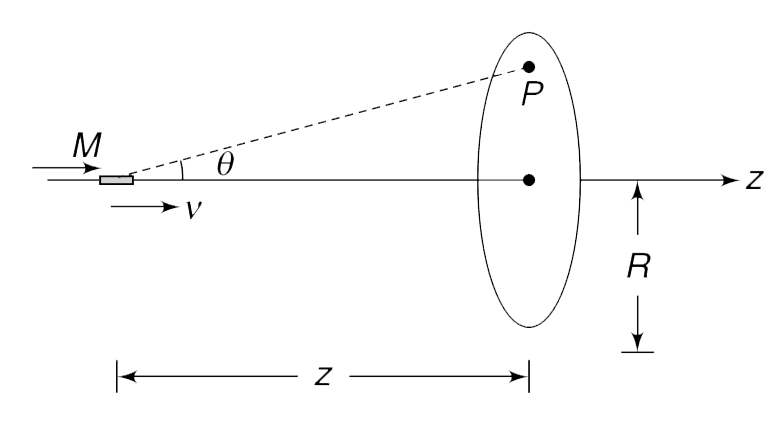
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
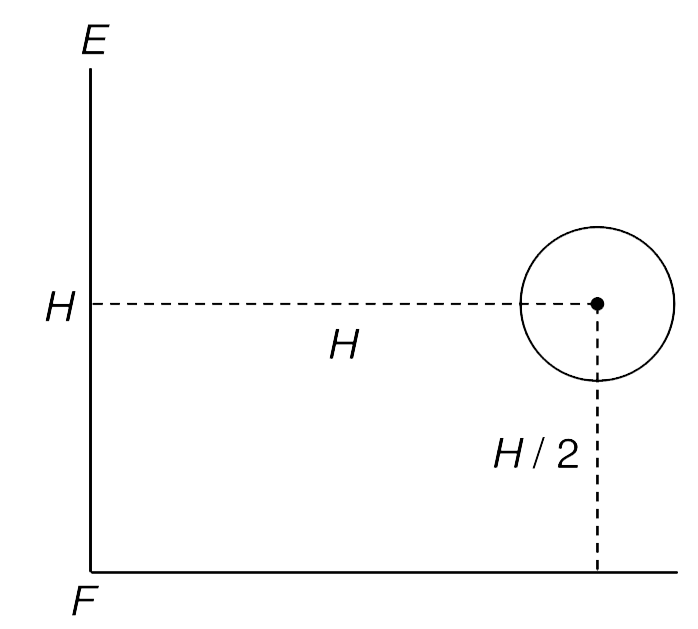
View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
View SolutionThe kinetic energy of the electron in an orbit of radius r in hydrogen atom is ( e = electronic charge)
View SolutionAn electron of charge e has a time period of revolution of T in a Bohr orbit of radius r. The dipole moment of the electron is
View SolutionAn electron of mass m and charge -e moves in circular orbit of radius r round the nucleus of charge +Ze in unielectron system. In CGS system the potential energy of electron is
View Solutionनाभिका के चारों ओर वृत्तीय कक्षा में घूमते हुए इलेक्ट्रॉन (आवेश e , द्रव्यमान m ) का कक्षीय वेग v , आवर्तकाल T तथा पथ की त्रिज्या r है ।

View SolutionAn electron revolve round the nucleous with the radius of the circular orbit is 'r' . To double the kinetic energy of the electron its orbital radius will be
View SolutionAn electron of charge 'e' is revolving in a circular orbit of radius r around a nucleus with speed v. The equivalent current is
View SolutionIf m and e are the mass and charge of the revolving electron in the orbit of radius r for hydrogen atom, the total energy of the revolving electron will be :
View SolutionThe kinetic energy of the electron in an orbit of radius r in hydrogen atom is (e = electronic charge)
View SolutionWhen an electron of charge , e and mass , m moves with velocity v around the nuclear charge 'Ze' describing the circular orbit, the potential energy of the electron is
View SolutionWhen an electron with charge .e. and mass .m. moves with velocity .v. around the nucleus having nuclear charge .Z. in a circular orbit of radius .r., the potential energy of electron is
View Solutionm द्रव्यमान का एक उपग्रह,M द्रव्यमान के ग्रह के चारों ओर R त्रिज्या की वृत्तीय कक्षा में घूम रहा है, तो इसकी कुल ऊर्जा E होगी :
View Solution
