A vector A makes on angle 30° with the y-axis in anticlockwise direction. Another vector B makes on angle 30° with the x-axis in clockwise direction. Find angle between yectors A and B.
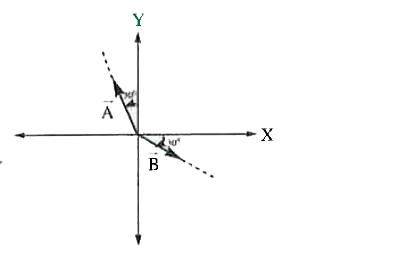
From the diagram the angle between →Aand→B is 30∘+90∘=150∘
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
View SolutionWrite down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
View SolutionA vector 3i + 4j rotates about its tail through an angle 37° in anticlockwise direction then the new vector is
View SolutionA vector makes an angle of π4 with each of x-axis and y-axis Find the angle made by it with the z-axis.
View SolutionA unit vector a makes an angle π4 with z-axis. If a+i+j is a unit vector, then a can be equal to
View SolutionA unit vector a makes an angle π4 with z-axis. If a+i+j is a unit vector, then a can be equal to
View SolutionA displacment vector fo magnitude 4 makes an angle 30∘ with the x-axis. Its rectangular components in x-y plane are
View SolutionWrite down a unit vector in XY plane, making an angle of 30∘ with positive direction of x-axis.
View SolutionA line passing through the point A(3,0) makes 300 angle with the positive direction of x- axis . If this line is rotated through an angle of 150 in clockwise direction, find its equation in new position.
View SolutionA line through the point A(2,0) which makes an angle of 300 with the positive direction of x-axis is rotated about A in clockwise direction through an angle 150. Find the equation of the straight line in the new position.
View Solution
