A vector is not changed if
it is rotated through an arbitrary angle
it is multiplied by an arbitrary scalar
it is cross multiplied by a unit vector
it is displaced paralled to itself
The correct Answer is:D
To solve the question "A vector is not changed if," we need to analyze each of the given options and determine which one does not alter the vector.
Step 1: Understand the nature of vectors
A vector is defined by both its magnitude and direction. Any operation that changes either of these two characteristics will change the vector itself.
Step 2: Analyze Option 1 - Rotated through an arbitrary angle
When a vector is rotated through an arbitrary angle, its direction changes. Therefore, the vector is not the same after rotation.
- Conclusion: Option 1 is incorrect.
Step 3: Analyze Option 2 - Multiplied by an arbitrary scalar
Multiplying a vector by a scalar changes its magnitude. Even if the direction remains the same, the vector's length changes, which means it is not the same vector.
- Conclusion: Option 2 is incorrect.
Step 4: Analyze Option 3 - Cross multiplied by a unit vector
Cross multiplying a vector by another vector (including a unit vector) results in a new vector that is perpendicular to both original vectors. This operation changes the direction and magnitude of the original vector.
- Conclusion: Option 3 is incorrect.
Step 5: Analyze Option 4 - Displaced parallel to itself
Displacing a vector parallel to itself means moving it in the same direction without changing its magnitude or direction. This operation does not alter the vector, as it remains the same in terms of both magnitude and direction.
- Conclusion: Option 4 is correct.
Final Answer:
A vector is not changed if it is displaced parallel to itself (Option 4).
---
A vector is defined by both its magnitude and direction. Any operation that changes either of these two characteristics will change the vector itself.
When a vector is rotated through an arbitrary angle, its direction changes. Therefore, the vector is not the same after rotation.
- Conclusion: Option 1 is incorrect.
Multiplying a vector by a scalar changes its magnitude. Even if the direction remains the same, the vector's length changes, which means it is not the same vector.
- Conclusion: Option 2 is incorrect.
Cross multiplying a vector by another vector (including a unit vector) results in a new vector that is perpendicular to both original vectors. This operation changes the direction and magnitude of the original vector.
- Conclusion: Option 3 is incorrect.
Displacing a vector parallel to itself means moving it in the same direction without changing its magnitude or direction. This operation does not alter the vector, as it remains the same in terms of both magnitude and direction.
- Conclusion: Option 4 is correct.
A vector is not changed if it is displaced parallel to itself (Option 4).
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Subjective
24 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Example
40 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.3
4 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
(A): The direction of velocity vector remains unchanged though the coordinate system is changed
(R) : The direction of real vector is independent of coordinate system
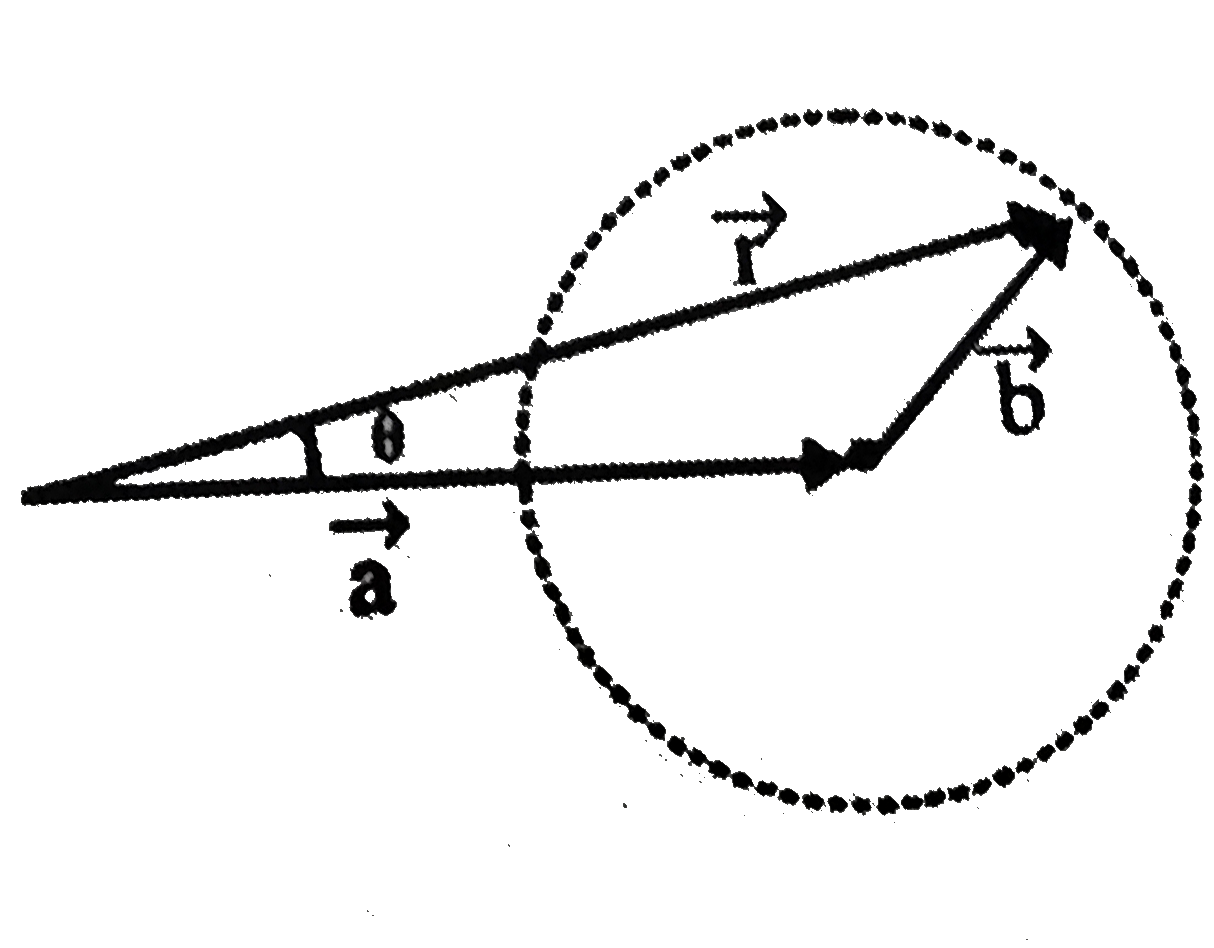
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View Solution
Knowledge Check
An impulse is supplied to a moving object with the force at an angle of 120∘ with respect to velocity vector. The angle between the impulse vector and the change in momentum vector is
A120∘B0∘C60∘D240∘
Asserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.
View SolutionA vector may change when we :
View SolutionA vector may change when we :
View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.
View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.
View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View Solution
