Question

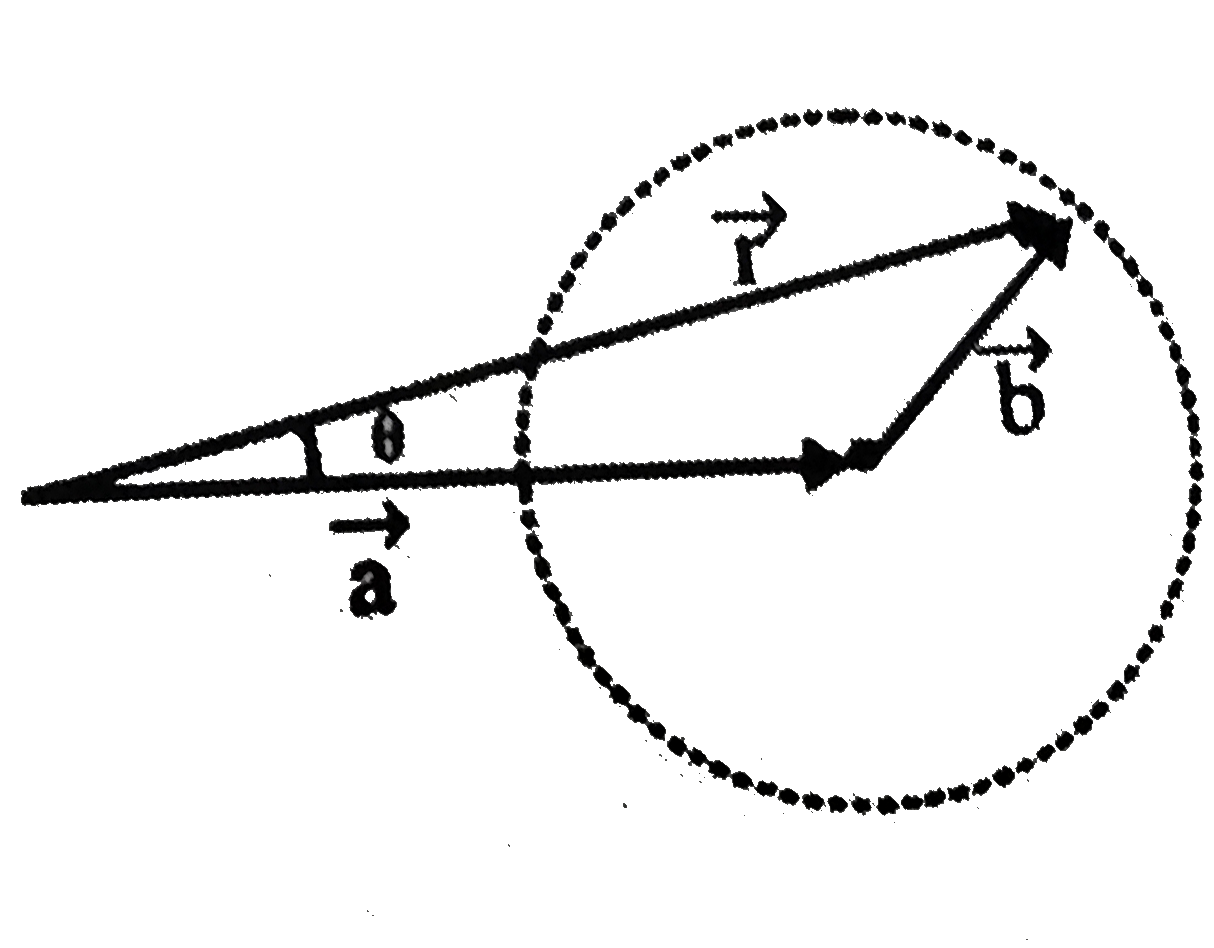
Keeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector $\overrightarrow{a}$ is kept constant. When vector $\overrightarrow{b}$ addede to $\overrightarrow{a}$ changes its direction, the tip of the resultant vector $\overrightarrow{r}=\overrightarrow{a}+\overrightarrow{b}$ describes circles of radius b with its centre at the tip of vector $\overrightarrow{a}$. Maximum angle between vector $\overrightarrow{a}$ and the resultant $\overrightarrow{r}=\overrightarrow{a}+\overrightarrow{b}$ is

Options

A. `tan^(-1)""((b)/(r))`
B. `tan^(-1)""((b)/(sqrt(a^(2)-b^(2))))`
C. `cos^(-1)(r//a)`
D. `cos^(-1)(a//r)`

Answer

A::C

Explanation

Angle between `vec(r)` and `vec(b)` is maximum when `vec(r)` is tangent to circle.