A vector rotates about its tail through an angle in clock wise direction then the new vector is
The magnitude of is the angle made by the vector with x-axis is
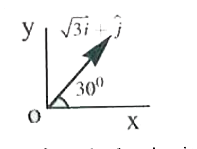
When the given vector rotates 30 in clock wise its direction changes along x - axis but its magnitude does not change.
The new vetor is

Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
A vector ˆi+√3ˆj rotates about its tail through an angle 60° in clockwise direction then the new vector is
View SolutionA vector 3i + 4j rotates about its tail through an angle 37° in anticlockwise direction then the new vector is
View SolutionA line passing through the point A(3,0) makes 300 angle with the positive direction of x- axis . If this line is rotated through an angle of 150 in clockwise direction, find its equation in new position.
View SolutionA vector →a=tˆi+t2ˆj is rotated through a righat angle passing through the x-axis. What is the vector in its new position (t>0)? (A) t2ˆi−tˆj (B) √tˆi−1√tˆj (C) −t2ˆi+tˆj (D) t2ˆi−tˆjt√t2+1
View SolutionA plane is parallel to the vectors ˆi+ˆj+ˆk and 2ˆk and another plane is parallel to the vectors ˆi+ˆj and ˆi−ˆk. The acute angle between the line of intersection of the two planes and the vector ˆi−ˆj+ˆk is
View SolutionThe vector −−→OA where O is origin is given by −−→OA=2ˆi+2ˆj . Now it is rotated by 45∘ anticlockwise about O . What will be the new vector . ?
View SolutionA vector of length l is turned through the angle θ about its tail. What is the change in the position vector of its head ?
View SolutionIf the vector −ˆi+ˆj−ˆk bisects the angle between the vector →c and the vector 3ˆi+4ˆj, then the vector along →c is
View SolutionThe angle made by the vector →A=ˆi+ˆj with x-axis is
View SolutionIf a vector ¯¯¯¯¯¯OP=3ˆi+3ˆj is turned clockwise by an angle of 15°, then the y-component of rotated vector would be
View Solution
