A vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
A
ˆi+ˆj
B
4ˆj
C
ˆj+ˆk
D
−7ˆk
Video Solution
Text Solution
The correct Answer is:D
The vector product of two non-zero vectors is zero of they are in the same direction or in the opposite direction. Hence vector →B must be parallel or antiparallel to vector →A. along ±z - axis
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (MOTION IN A PLANE )23videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (PROJECTILE MOTION)58videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (VECTORS)23videos
KINEMATICS
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS32videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)24videos
LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A vector →A is along the positive x-axis and its vector product with another vector →B is zero, then vector →B could be
Aˆi+ˆjB4ˆiCˆj+ˆkD−7ˆk - Question 2 - Select One
A vector →A is along the positive x- axis . If B is another vector such that →A×→B is zero , then B could be
A4jB−4iC−(i+j)D(j+k) - Question 3 - Select One
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
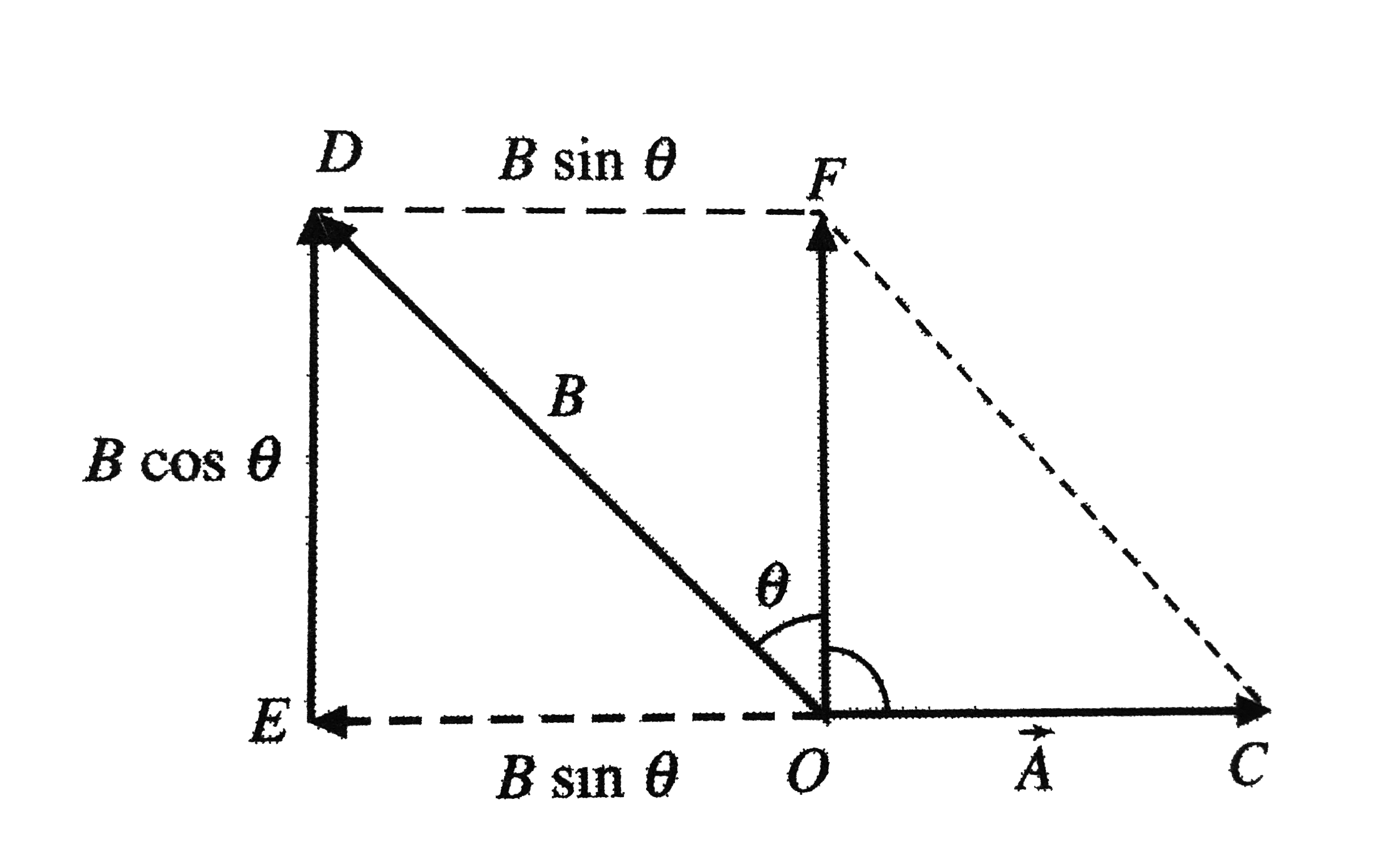 .A120B90C60D150
.A120B90C60D150
The magnitude of the vector product of two vectors →A and →B may not be:
View SolutionA vector →A makes an angle 30∘ with the Y-axis in anticlockwise direction. Another vector →B makes an angle 30∘ with the x-axis in clockwise direction. Find angle between vectors →A and →B.
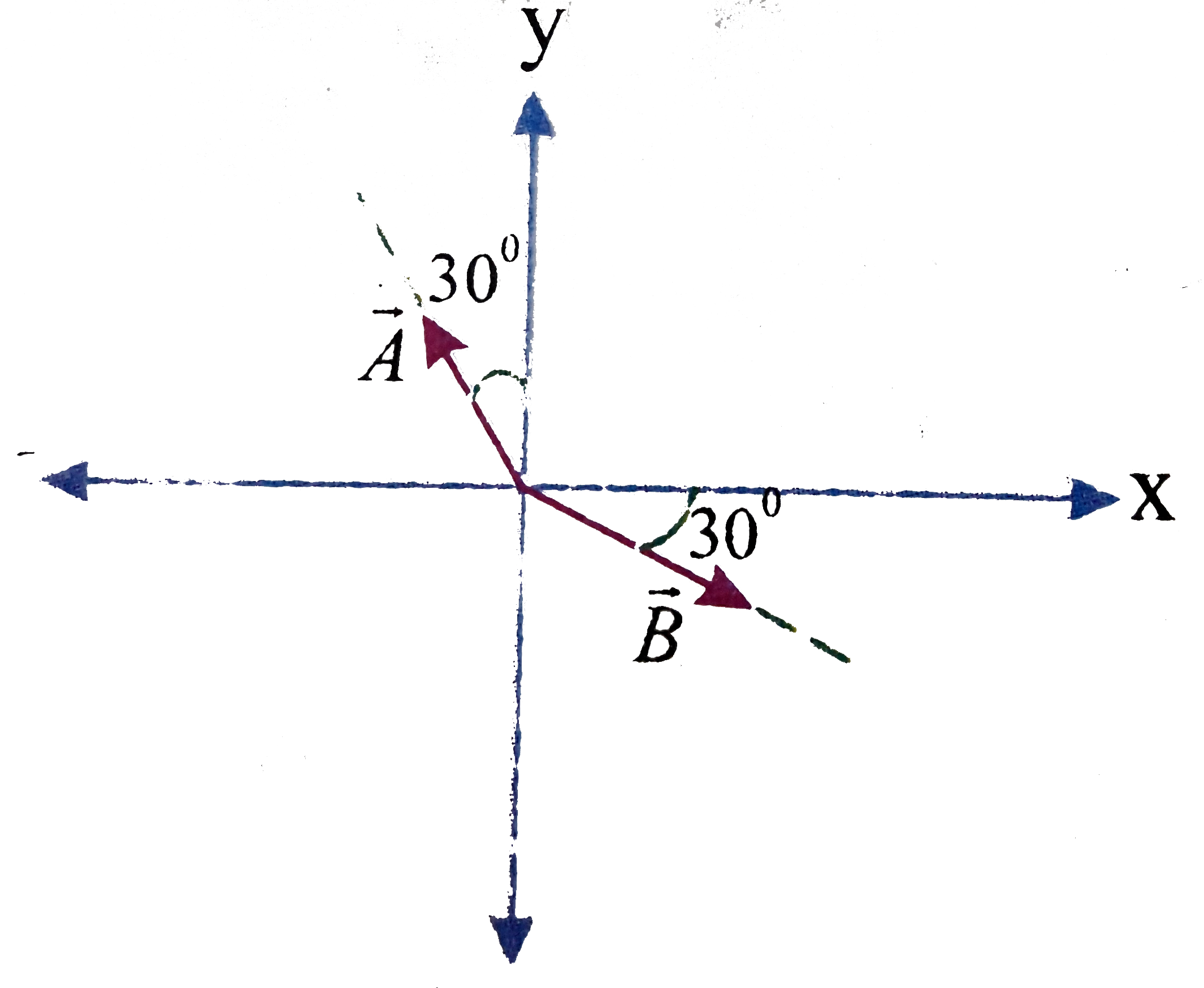 View Solution
View SolutionThe magnitude of the vectors product of two vectors ∣∣→A∣∣and∣∣→B∣∣ may be
View SolutionVector →A−→B represents -
View SolutionResolved part of vector →a and along vector →b is →a1 and that prependicular to →b is →a2 then →a1×→a2 is equl to
View Solution

