A vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
6√5
12√5
16√5
8√5
The correct Answer is:D
(d) According to given condition ,
A+Bˆi=Rˆj(where,R is the resukltant vector)
Also , R=2B
∴A+Bˆi=2BˆjorA=Bˆj=Bˆi
∴A2=4B2+B2=5B2
Here,A=8
∴64=5B2
⇒B=√645=8√5
Topper's Solved these Questions
Similar Questions
Vector →A, which is directed along an x axis , is to be added to vector →B, which has a magnitude of 7.0m. The sum is a third vector that is directed along the y axis, with a magnitude that is 3.0 times that of →A. What is that magnitude of →A ?
View SolutionVector →A, which is directed along an x axis, is to be added to vector →B, which has a magnitude of 6.0 m. The sum is a third vector that is directed along the y axis, with a magnitude of →AFind the magnitude of →A ?
View Solution
Knowledge Check
A vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
A√10B10C5D√5A vector →A is along the positive x- axis . If B is another vector such that →A×→B is zero , then B could be
A4jB−4iC−(i+j)D(j+k)If →i and →j are unit vectors along x-axis and y-axis respectively, the magnitude of vector →i+→j will be :-
A1B√2C√3D2
If the resultant of →a and →b lie along y-axis. Find thre magnitude of b
View SolutionA vector vec Awhenadded→the→−−→r vec B = 3. 0 hat i+ 4 hat jyieldsarestant–––––→−−→rtˆis∈thepositivey−directionandhasamagn∫udeequal→tˆof vec B.F∈dthemagnitudeof vec A .
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
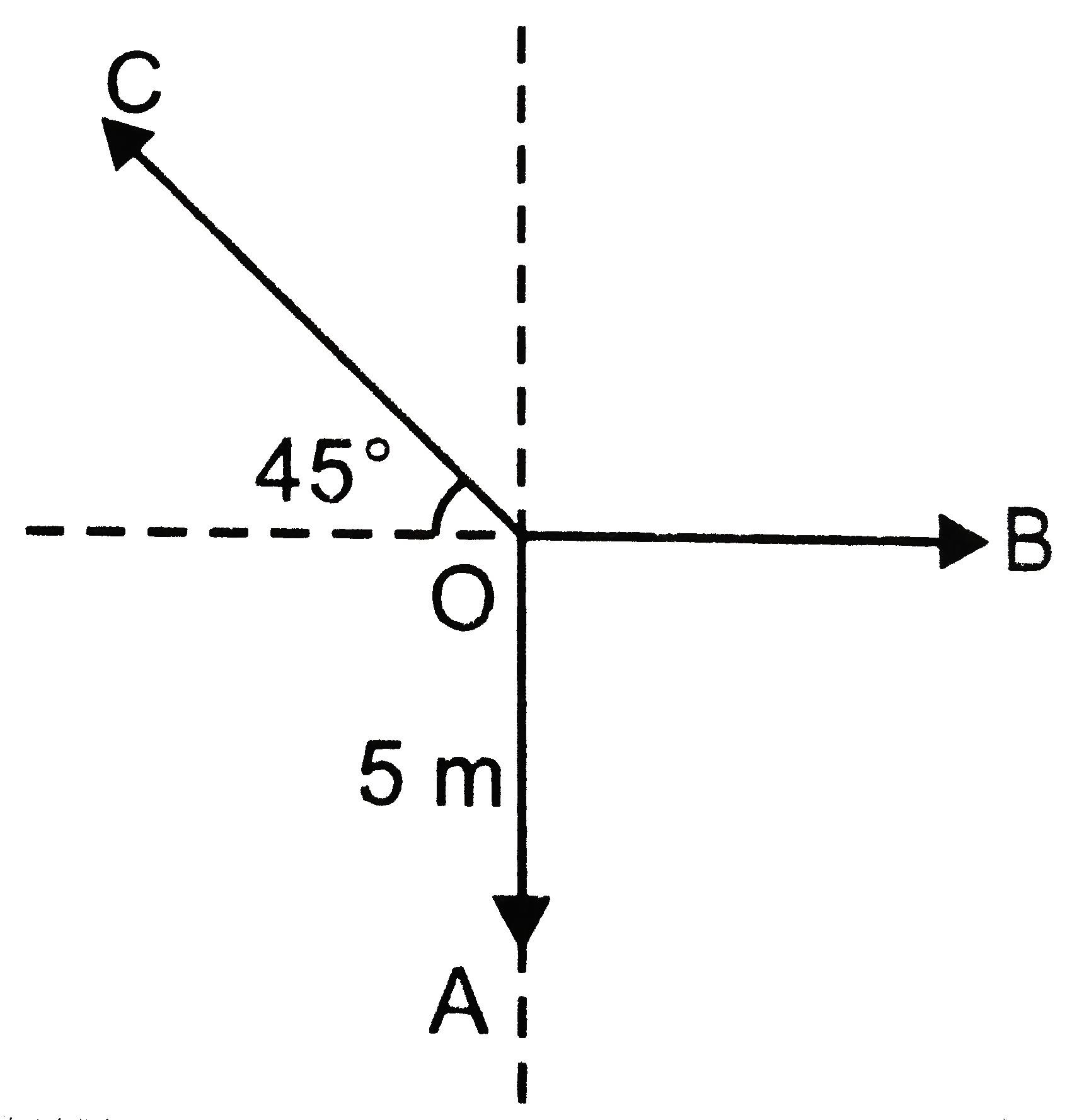 .
.
(a) What is the magnitude of the vector −−→OB?<br>(b)Wˆisthemagnitudeofthe→−−→r vec (OC) ?
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
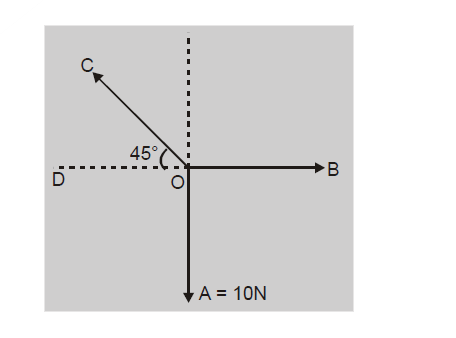
(ii) What is the magnitude of vector −−→OC ?
View SolutionWrite the magnitude of the vector →a in terms of dot product.
View Solution
