Write the magnitude of the vector →a in terms of dot product.
The correct Answer is:√→a.→a
Step by step video, text & image solution for Write the magnitude of the vector vec(a) in terms of dot product. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - Ncert File Question from Ncert Book (Exercise 10.1)
5 Videos
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - Ncert File Question from Ncert Book (Exercise 10.2)
19 Videos
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - Objective Type Questions (C. True/False Questions)
10 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - CHAPTER TEST 11
11 Videos
Similar Questions
Knowledge Check
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8The maximum value of the magnitude of the resultant of two vectors →Pand→Q is 24 units and the minimum value of the magnitude of their resultant is 4 units. What is the ratio of the magnitudes of the vectors →Pand→Q ?
A34B45C65D75
The sum and difference of two vectors →A and →B are ,→A+→B=2ˆi+6ˆj+ˆk and →A−→B=4ˆi+2ˆj−11ˆk. Find the magnitude of each vector and their scalar product →A.→B.
View SolutionVector - Dot Product
View SolutionThe sum and difference of two vectors →A and →B are →A+→B=2ˆi+6ˆj+ˆk and →A−→B=4ˆi+2ˆj−11ˆk. Find the magnitude of each vector and their scalar product →A→B.
View SolutionThe resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
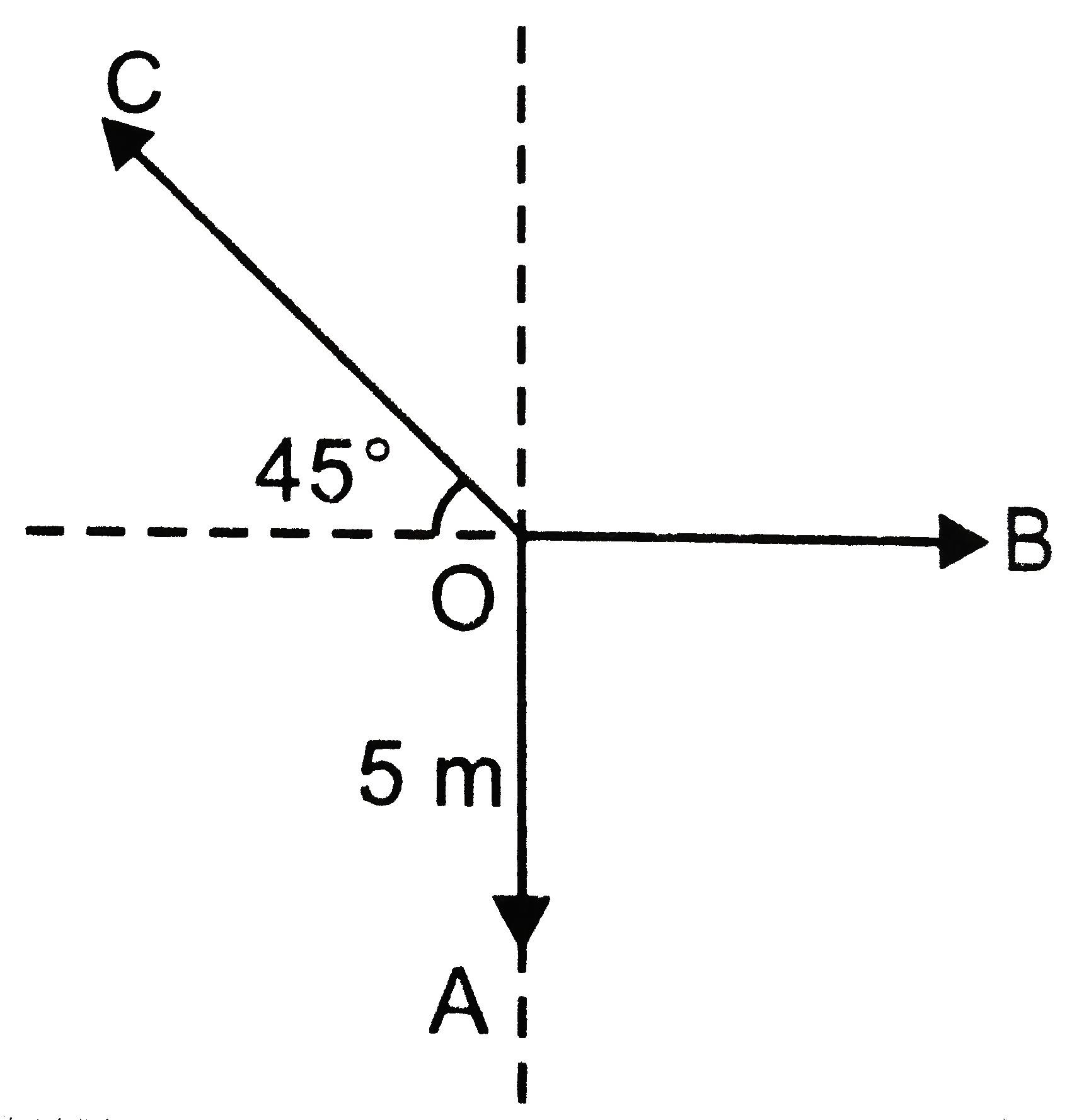 .
.
(a) What is the magnitude of the vector −−→OB?<br>(b)Wˆisthemagnitudeofthe→−−→r vec (OC) ?
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
View Solution
