A voltage V is applied to a dc electric motor. The armature winding resistance is equal to R. At what value of current flowing through the winding resistance is equal to R. At what value of current flowing through the winding will the useful power of the motor be the highest ? What is it equal to? What is the motor efficiency in this case ?
To solve the problem, we need to find the current at which the useful power of the DC motor is maximized, the value of that maximum power, and the motor's efficiency at that point.
1. Understanding the Circuit:
The total voltage V is applied across the armature resistance R and the load resistance R0 (the motor's load). The total current I flowing through the circuit can be expressed using Ohm's Law:
I=VR+R0
2. Calculating the Power Delivered to the Motor:
The power delivered to the motor (which is the useful power) can be calculated using the formula for power:
P=I2R0
Substituting the expression for current I:
P=(VR+R0)2R0
Simplifying this gives:
P=V2R0(R+R0)2
3. Finding Maximum Power:
To find the value of R0 that maximizes the power P, we can use the condition that maximum power transfer occurs when the load resistance R0 is equal to the armature resistance R:
R0=R
Substituting R0=R into the power equation:
Pmax=V2R(R+R)2=V2R(2R)2=V2R4R2=V24R
4. Calculating Motor Efficiency:
The input power to the motor can be calculated as:
Pinput=V⋅I=V⋅VR+R0=V2R+R0
Substituting R0=R:
Pinput=V2R+R=V22R
The efficiency η of the motor is given by the ratio of the useful power to the input power:
η=PmaxPinput=V24RV22R=1/41/2=12=0.5
Converting this to percentage:
η=0.5×100%=50%
Final Answers:
- The current at which the useful power is maximized is when R0=R.
- The maximum useful power is Pmax=V24R.
- The motor efficiency at this point is 50%.
The total voltage V is applied across the armature resistance R and the load resistance R0 (the motor's load). The total current I flowing through the circuit can be expressed using Ohm's Law:
I=VR+R0
The power delivered to the motor (which is the useful power) can be calculated using the formula for power:
P=I2R0
Substituting the expression for current I:
P=(VR+R0)2R0
Simplifying this gives:
P=V2R0(R+R0)2
To find the value of R0 that maximizes the power P, we can use the condition that maximum power transfer occurs when the load resistance R0 is equal to the armature resistance R:
R0=R
Substituting R0=R into the power equation:
Pmax=V2R(R+R)2=V2R(2R)2=V2R4R2=V24R
The input power to the motor can be calculated as:
Pinput=V⋅I=V⋅VR+R0=V2R+R0
Substituting R0=R:
Pinput=V2R+R=V22R
The efficiency η of the motor is given by the ratio of the useful power to the input power:
η=PmaxPinput=V24RV22R=1/41/2=12=0.5
Converting this to percentage:
η=0.5×100%=50%
- The current at which the useful power is maximized is when R0=R.
- The maximum useful power is Pmax=V24R.
- The motor efficiency at this point is 50%.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Knowledge Check
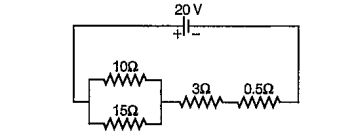
In the circuit, the current flowing through 10Ω resistance is
 A12AB1.2AC0.8AD0.4A
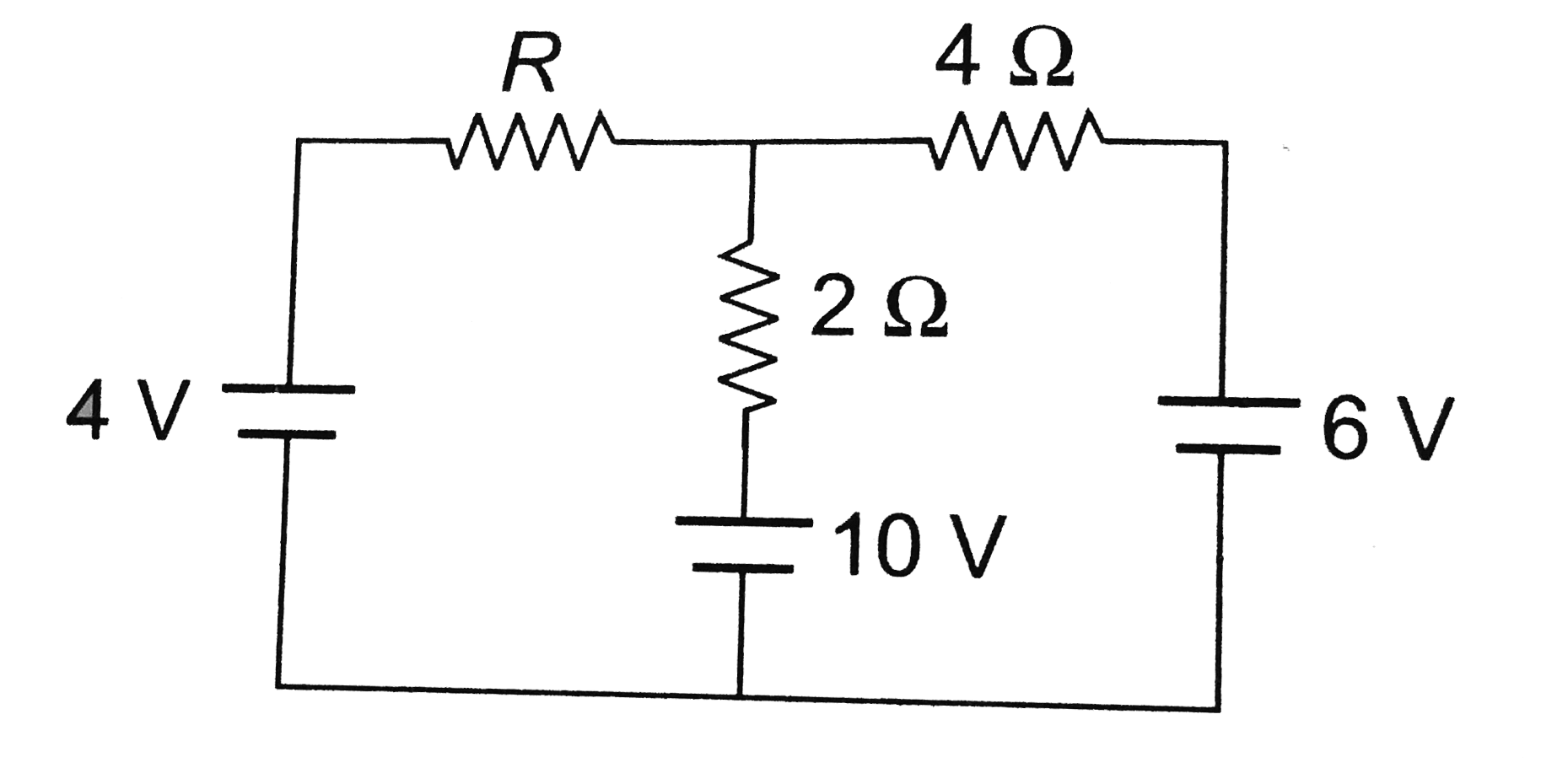
A12AB1.2AC0.8AD0.4AFind the value of R for which no current will flow through 5V battery
 A4ΩB1ΩC3ΩD4Ω
A4ΩB1ΩC3ΩD4ΩA sinusoidal A.C. current flows through a resistor of resistance 10Ω. If the peak current is 2A flowing through the resistor, then the power dissipated is_________W.
A30B20C10D40
For what value of R in circuit , current through 4Ω resistance is zero.
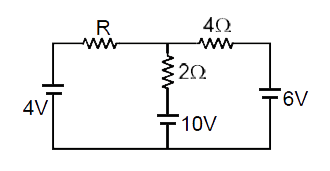
View Solution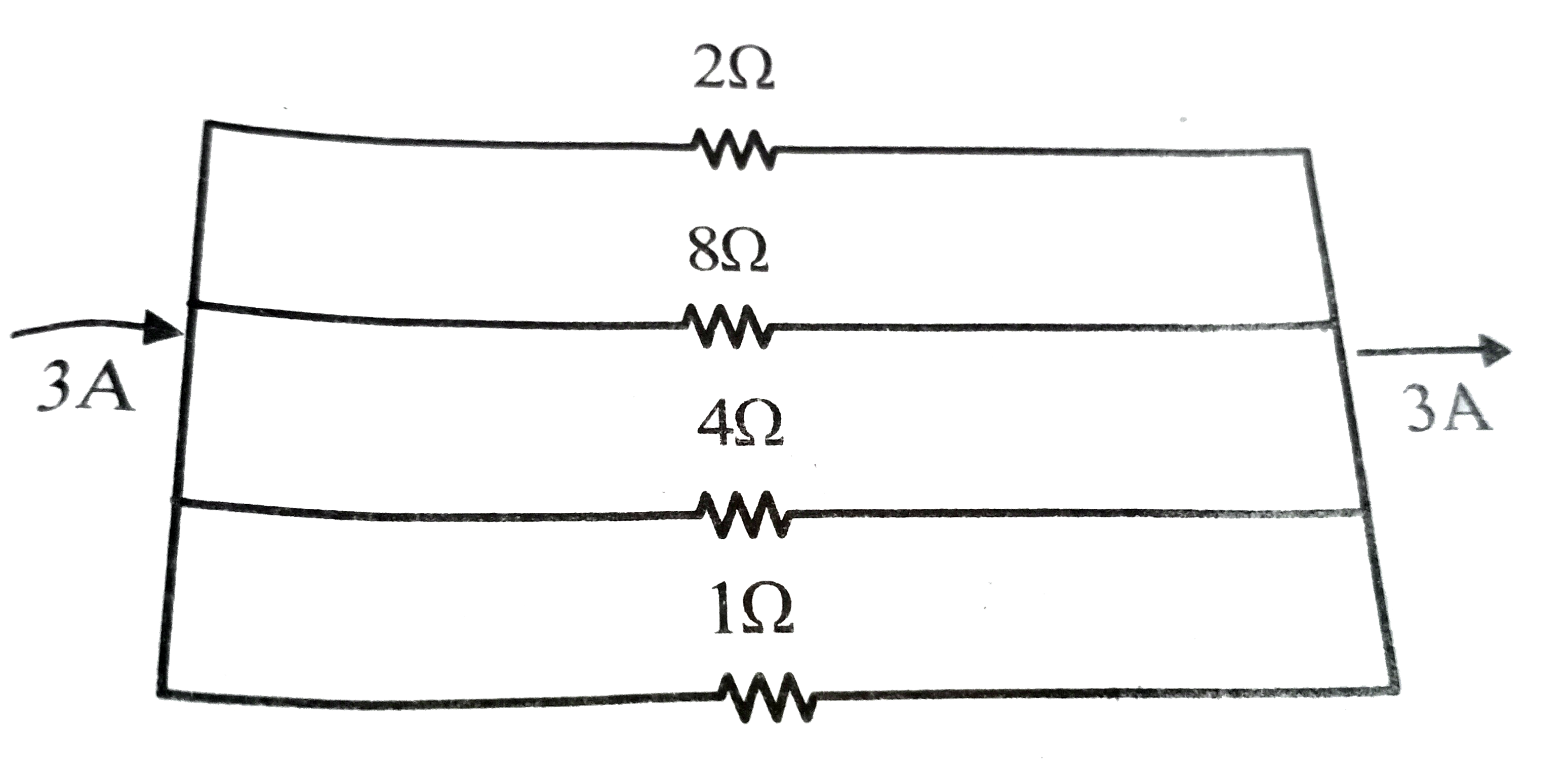
If an input current 3 A flows through the circuit shown above. What is the value of the current flowing through the 4Ω resistor ?
View SolutionCalculate the current flows through resistance 2Ω.
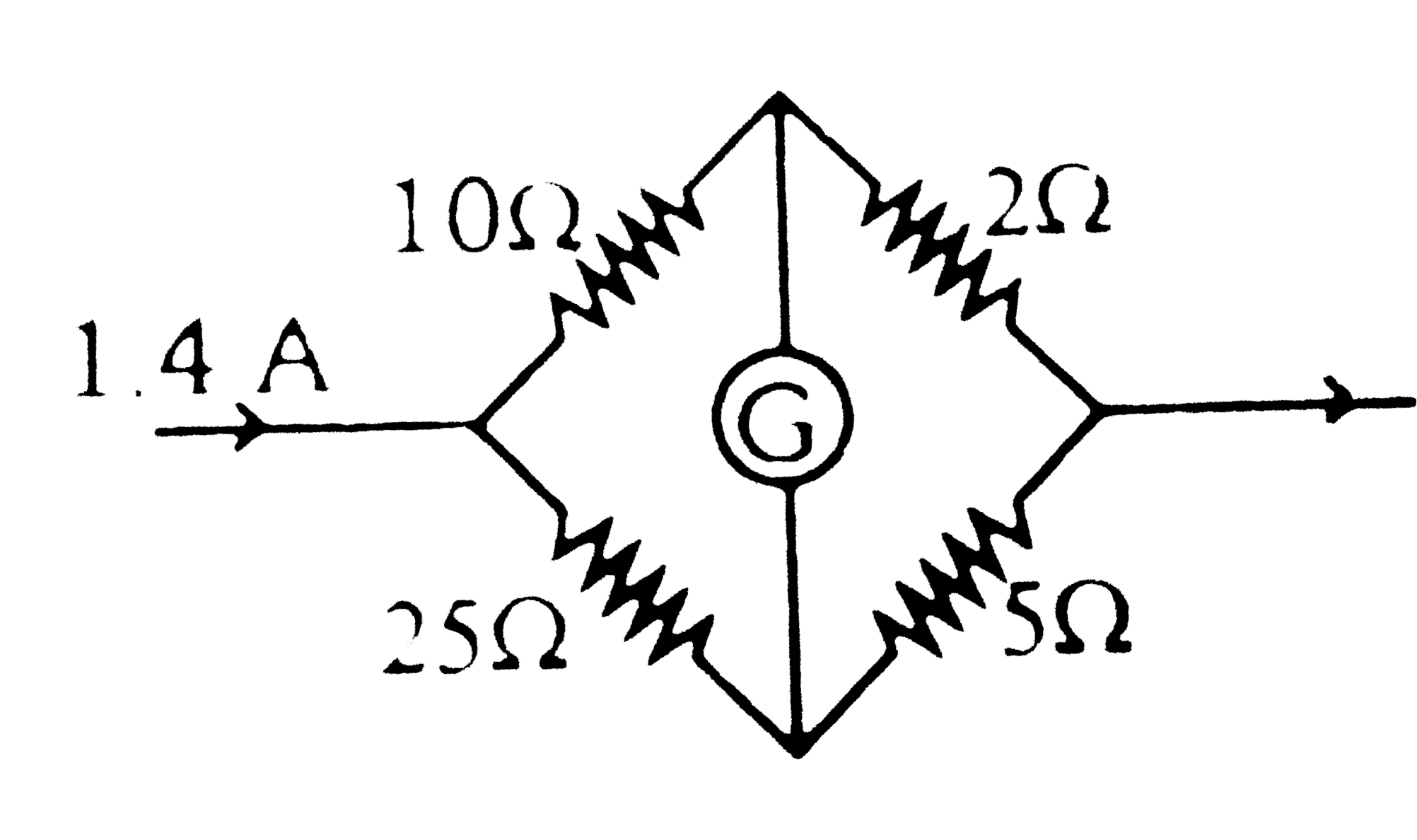
View SolutionA voltage of 30V is applied across a carbon resistance with first, second and third strips or bonds. Find the value of current through the resistance.
View SolutionIn the given circuit current flowing through the resistance 20Ω is 0.3A, while the ammeter reads 0.8 A. What is the value of R1

View Solution